محیط و مساحت متوازی‌الاضلاع ؛ نحوه محاسبه + مثال های متنوع

در مقالات قبل، در مورد محیط و مساحت مربع و مستطیل مطالبی را بیان کردیم، حال در این متن می‌خواهیم در رابطه با نحوه محاسبه محیط و مساحت متوازی الاضلاع و وجه اشتراکی که با سایر اشکال هندسی دارد، صحبت کنیم و سپس با چند مثال ساده و کاربردی مطلب را به‌صورت‌کامل بپرورانیم.

اگر به دنبال تمامی فرمول های ریاضی مساحت و محیط ها هستید پیشنهاد میکنم مقاله مساحت و محیط اشکال هندسی را  مطالعه کنید.

با تیم آموزشی رایاد همراه باشید.

 

تعریف متوازی‌الاضلاع

متوازی الاضلاع چهارضلعی است که اضلاع آن دو به دو موازی هستند، دو زاویه باز و دو زاویه تند دارد و خط تقارن و قطر یکسان‌هم ندارد. در متوازی‌الاضلاع زوایای روبرو باهم برابرند و زوایای کناری مکمل، هم‌چنین در این شکل قطرها هم‌دگیر را نصف می‌کنند.

 

 

محیط متوازی الاضلاع

همانطور که قبلا نیز گفته شد، به دو تا دور یک شکل محیط آن شکل گفته می‌شود. برای محاسبه محیط متوازی‌الاضلاع باید از رابطه زیر استفاده کرد:

۲*(مجموع دو ضلع مجاور) = محیط 

 

 

مساحت متوازی ‌الاضلاع

اگر از یک رأس متوازی‌الاضلاع، خطی عمود بر ضلع مقابل رسم کنیم، ارتفاع متوازی‌الاضلاع را رسم کرده ایم. به ضلعی که ارتفاع برآن رسم شده، قاعده می‌گوییم.

حال برای محاسبه مساحت متوازی‌الاضلاع از فرمول زیر استفاده می‌کنیم.

 قاعده * ارتفاع = مساحت متوازی‌الاضلاع

 

 

فیلم های کمک آموزشی رهپویان از بهترین ابزارهای کمک آموزشی هستند که فرایند یادگیری را برای دانش آموزان میسر می سازند و زمینه را برای فهم عمیق مطالب ریاضی مهیا میکنند.

برای دسترسی و تهیه ی این مجموعه آموزشی بر روی لینک فیلم های آموزشی رهپویان کلیک نمایید.

 

تبدیل متوازی الاضلاع به مستطیل

برای درک بهتر نحوه محاسبه مساحت متوازی‌الاضلاع فعالیت زیر را انجام دهید:

• ارتفاع متوازی‌الاضلاع را رسم کنید.

 

 

• حال با دقت به شکل نگاه کنید، یک مثلث درون شکل ساخته شده است.
• مثلث را سمت دیگر شکل حرکت دهید.

 

 

• متوازی‌الاضلاع به مستطیل تبدیل شده است و ما می‌دانیم مساحت مستطیل برابر است با حاصلضرب طول در عرض
• که در این شکل عرض مستطیل ارتفاع متوازی‌الاضلاع و طول مستطیل قاعده این چهارضلعی است.

 

در ادامه برای درک بهتر مفاهیم، چندین نمونه سوال از محیط و مساحت متوازی‌الاضلاع را با هم حل می‌کنیم.

 

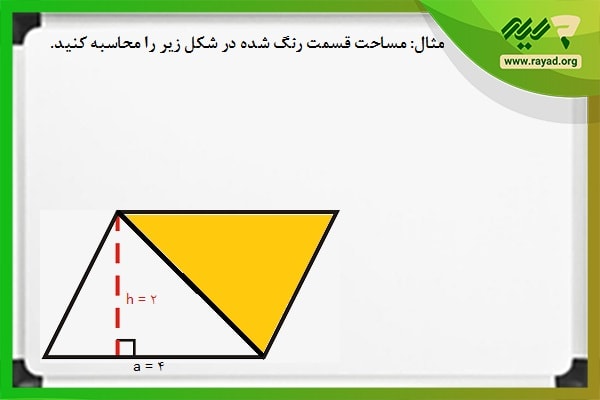
مثال ۱:در یک متوازی‌الاضلاع اندازه قاعده ۴ متر و اندازه ارتفاع ۲ متر است، مساحت متوازی‌الاضلاع چند مترمربع است؟

 

 

همانطور که قابل مشاهده است این مثال یک نمونه ساده و ابتدایی از مساحت متوازی‌الاضلاع است که برای حل سوال باید فرمول مساحت متوازی الاضلاع را بنویسید و جایگذاری کنید.

 

 

مثال۲: اندازه قاعده یک متوازی‌الاضلاع برابر با ۵ سانتی‌متر و اندازه ضلع دیگر برابر ۳ سانتی‌متر است. محیط شکل را بدست آورید.

 

 

برای پاسخ به این سوال باید  ابتدا فرمول را نوشته، سپس جایگذاری کنید.

 

 

مثال ۳: می‌خواهیم دور تا دور زمین متوازی‌الاضلاع شکلی که برای بازی کودکان در حیاط مدرسه درست کرده‌ایم را، درخت‌کاری کنیم. مدیر مدرسه اندازه قاعده زمین را ۷ متر و اندازه ضلع مجاور آن را ۴ متر به کارگر داده است. کارگر چند متر را باید گل کاری کند؟

 

 

همیشه به دور تا دور یک شکل، محیط آن شکل می‌گوییم و برای محاسبه تنها نیاز به نوشتن فرمول و جایگذاری داریم. حتی اگر آخر سوال حرفی از محیط نمی‌زد، باز هم چون به دور تا دور شکل اشاره کرده یعنی محیط مدنظرش بوده است.

 

 

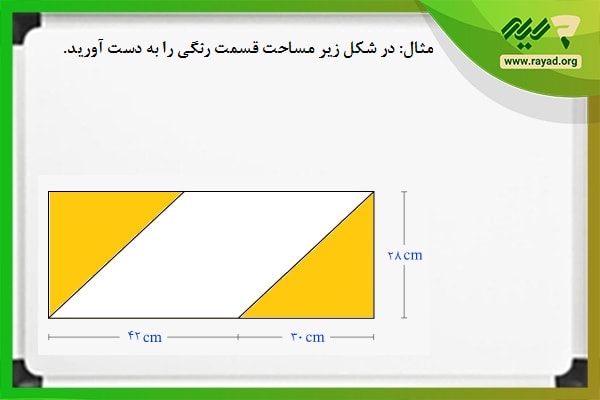
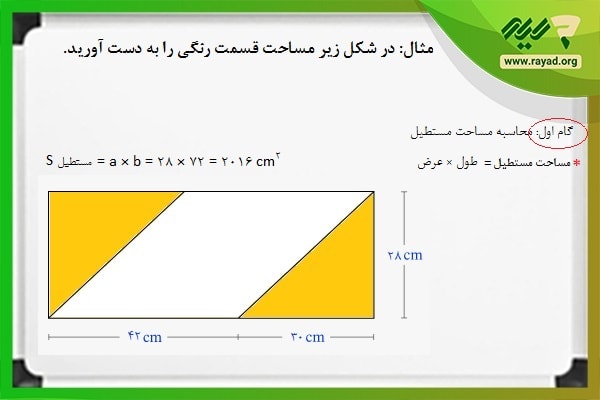
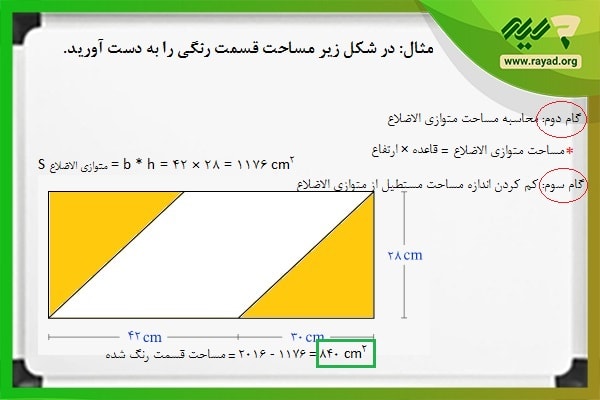
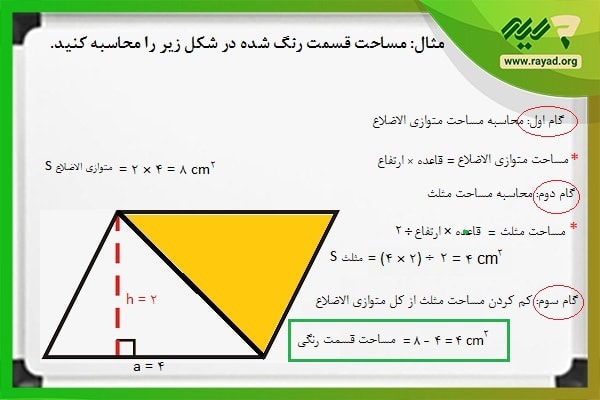
مثال۴: مساحت کل شکل‌ زیر را بدست آورید.

 

 

در آموزش های قبلی نمونه این سوالات را با هم حل کرده بودیم، برای اینکه بتوانید مساحت کل شکل را بدست آورید باید به طور مجزا مساحت هر شکل را حساب کنید و سپس مقدار نهایی را باهم جمع کنید.

 

برای آشنایی با نرم افزارها و فیلم های آموزشی ریاضی چهارم دبستان بر روی باکس های زیر کلیک کنید.

مثال ۵: فرض کنید زمین متوازی‌اضلاعی داریم که قرار است کل سطح آن را گل‌های داوودی بکاریم. اگر اندازه قاعده ۳ متر و ارتفاع آن ۵ متر باشد،  چند متر مربع را باید گل کاری کنیم؟

 

 

اگرچه کمی صورت سوال تغییر کرده اما میدانیم که سطح زمین که قرار است گل‌کاری شود همان مساحت است. پس طبق فرمول مساحت متوازی الاضلاع پیش می‌رویم.

 

 

یکی از روش های نوین آموزشی بهره مندی دانش آموزان از نرم افزارهای کمک آموزش می باشد. کیف الکترونیک آریا از جمله نرم افزارهای آموزش ابتدایی می باشد که فرایند یادگیری را اسان و دلپذیر نموده است.

برای آشنایی بیشتر با این محصول آموزشی بر روی لینک خرید کیف آریا کلیک نمایید.

 

اشتراک متوازی الاضلاع با سایر اشکال

تعریف بسیاری از اشکال هندسی از متوازی الاضلاع گرفته می‌شود. برای مثال به متوازی‌الاضلاعی که همه ی زوایای آن قائمه باشد، مستطیل می‌گوییم، یا متوازی الاضلاعی که هرچهار ضلع آن با هم برابر باشد، یک لوزی است و یا متوازی الاضلاعی که زوایای آن قائمه باشد و اضلاع آن با هم برابر باشند، یک مربع می‌یاشد.

 

شباهت متوازی الاضلاع با مستطیل

در هردو شکل اضلاع و زوایای روبرو دوبه‌دو با هم برابرند و قطرها علی‌رغم اینکه هم‌دیگر را نصف می‌کنند، بر هم عمود نیستند.

 

شباهت متوازی‌الاضلاع با لوزی

•  قطرها در شکل لوزی و متوازی‌الاضلاع با هم یکسان نیستند.
•  زاویه تند و باز در هر دو شکل دیده می‌شود.