محیط و مساحت مثلث متساوی الساقین

مثلث متساوی الساقین را در مقاله انواع مثلث معرفی کردیم.

حال در این مقاله قصد داریم با ویژگی‌های بیشتری از این مثلث آشنا شده و نحوه محاسبه محیط و مساحت آن را با استفاده از چند مثال کاربردی آموزش بدهیم.

پس از پایان این مقاله حتما شما به خوبی با متساوی الساقین آشنا شده و به راحتی مسائل مربوط به آن را حل می کنید.

با رایاد تا انتهای مقاله جذاب همراه باشید.

 

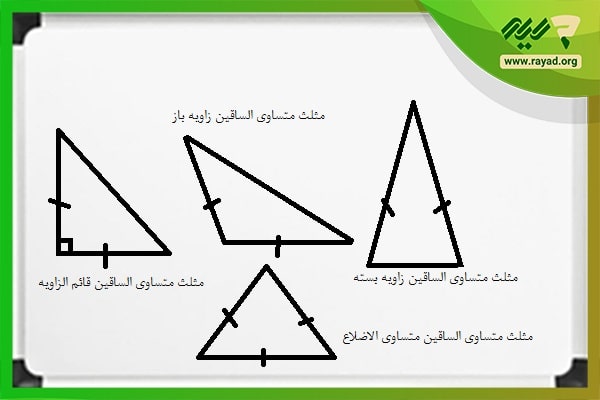
ویژگی های مثلث متساوی الساقین

به طور کلی، این مثلث، مثلثی است که اندازه دو ضلع آن با هم برابر بوده و ضلع دیگر مثلث که با آن دو ضلع برابر نیست، قاعده مثلث نام دارد.

همچنین اندازه زاویه های مثلث متساوی الساقین که مجاور به ساق‌های برابر هستند، با همدیگر برابر است. با این تفاسیر در این مثلث دو زاویه برابر و یک زاویه با اندازه متفاوت داریم.

از دیگر ویژگی‌های مهم این مثلث می‌توان به موارد زیر اشاره کرد:

• در متساوی الساقین، نیمساز، عمود منصف و ارتفاع رسم شده از راس بالایی مثلث روی هم منطبق هستند.
• نیمساز خارجی راس مثلث‌های متساوی الساقین با قاعده موازی بوده و برابر با زاویه های مجاور به ساق های برابر میباشد.

 

شکل مثلث متساوی الساقین

متساوی الساقین انواع مختلفی می‌تواند داشته باشد. در واقع، هر مثلثی به شرطی که دو ضلع برابر داشته باشد، متساوی الساقین به شمار می‌آید.

از این رو می‌توان گفت که مثلث متساوی الاضلاع یا حتی مثلث قائم الزاویه نیز نوعی متساوی الساقین هستند. در ادامه به بررسی فرمول‌ها و روش‌های محاسبه محیط و مساحت مثلث متساوی الساقین خواهیم پرداخت.

 

 

محیط مثلث متساوی الساقین

محیط مثلث متساوی الساقین مانند تمام مثلث‌های دیگر از جمع اندازه ۳ ضلع آن به دست می‌آید.

در این اشکال هندسی معمولا اندازه یکی از ساق‌های برابر به همراه قاعده مثلث داده می‌شود و از آنجایی که اندازه دو ساق در این مثلث با هم برابر هستند، پس می‌توان اندازه ۳ ضلع با هم جمع کرده و محیط شکل را به دست آورد.

فرمول محیط متساوی الساقین = مجموع اندازه ۳ ضلع

این رابطه به زبان نمادهای ریاضیاتی به صورت زیر خواهد بود:

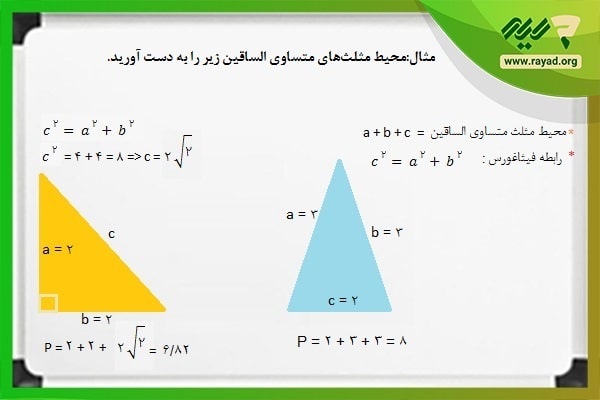
P = a + b + c

در این رابطه P محیط مثلث و a، b و c به ترتیب اضلاع مثلث هستند.

مثال:‌

محیط مثلث‌های متساوی الساقین زیر را به دست آورید.

 

 

برای محاسبه محیط مثلث‌ متساوی الساقین فوق اندازه هر ۳ ضلع را با هم جمع کنیم. در مثلث نارنجی برای پیدا کردن اندازه ضلع سوم یا وتر مثلث قائم الزاویه از رابطه فیثاغورس استفاده می‌کنیم. بنابراین خواهیم داشت:

 

 

 

 

آموزش ریاضی اگر اصولی و درست باشد، ریاضی را به یکی از درس‌های مورد علاقه دانش آموزان تبدیل خواهد کرد. استفاده درست از ابزارهای کمک آموزشی مسیر آموزش و یادگیری ریاضی را بسیار هموار می‌سازد. از جمله موثرترین ابزارهای کمک آموزشی برای  یادگیری مباحث ریاضی می‌توان به فیلم های آموزشی رهپویان دانش و اندیشه اشاره نمود.

این مجموعه با بهره‌گیری از جدیدترین متدهای آموزشی فضای جذابی را برای یادگیری دانش آموزان فراهم آورده است.

مساحت مثلث متساوی الساقین

مساحت مثلث‌ متساوی الساقین را می‌توان با ضرب قاعده در ارتفاع مثلث و تقسیم آن بر ۲ به دست آورد. به عبارت دیگر فرمول مساحت این مثلث برابر است با:

مساحت متساوی الساقین = (قاعده × ارتفاع) ÷ ۲

این فرمول بر اساس نمادهای ریاضیاتی به صورت زیر خواهد بود:

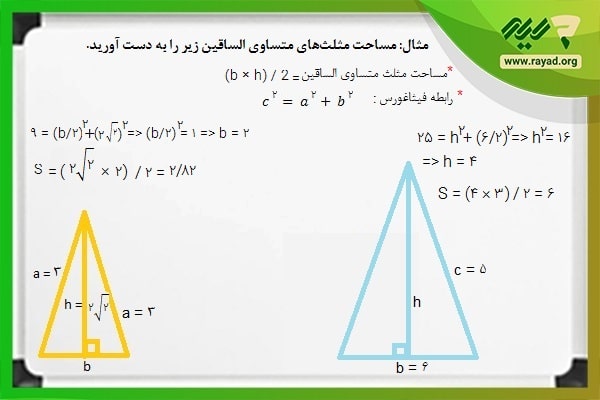
S = (b × h) / 2

در این رابطه S مساحت مستطیل و b و h به ترتیب قاعده و ارتفاع مثلث هستند. همچنین از آنجایی که گفتیم در متساوی الساقین ارتفاع و عمود منصف معادل هم هستند، به همین دلیل می‌توان با اطلاع از ارتفاع مثلث، مقدار قاعده آن را به دست آورد.به مثال زیر دقت کنید:

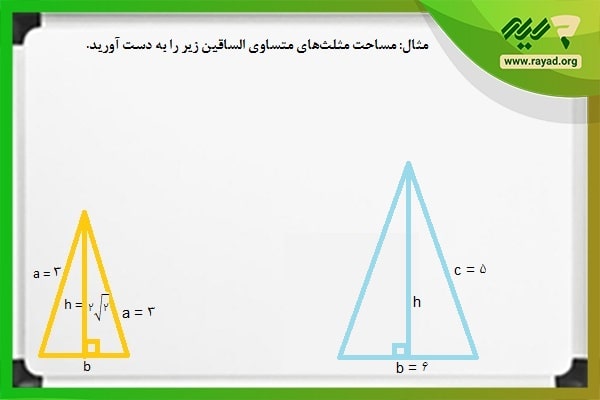
مثال:

مساحت مثلث‌های متساوی الساقین زیر را به دست آورید.

 

 

با توجه به توضیحات فوق می‌دانیم که ارتفاع متساوی الساقین قاعده آن را نصف می‌کند.

بنابراین در مثلث نارنجی می‌توانیم با استفاده از قضیه فیثاغورس در مثلث قائم الزاویه داخلی، اندازه نصف قاعده را به دست آورده، آن را دو برابر کنیم و در نهایت اندازه آن را برای محاسبه اندازه مساحت مثلث به کار ببریم.

در مورد مثلث آبی نیز با استفاده از همین رابطه می‌توانیم اندازه ارتفاع را به دست آورده و سپس آن را در فرمول مساحت مثلث متساوی الساقین قرار دهیم.

به این ترتیب پاسخ سوال به شرح زیر خواهد بود:

 

بیشتر بدانیم : مساحت و محیط اشکال هندسی

مثال:

فرض کنید می‌خواهیم سقف شیروانی ساختمانی را به ابعاد ۵، ۵ و ۶ متر و با استفاده از روکش‌های چوبی بسازیم. برای این کار به چه میزانی روکش چوبی احتیاج خواهیم داشت؟

 

 

برای محاسبه اندازه روکش مورد نیاز باید اندازه سطح قسمت جلویی این سقف را که به شکل مثلثی متساوی الساقین است محاسبه کنیم.

همان طور که در مثال قبل توضیح دادیم، برای محاسبه قاعده مثلث می‌توانیم از رابطه فیثاغورس استفاده کرده و اندازه آن را به دست آوریم.

در مرحله بعد اندازه ارتفاع و قاعده مثلث را در رابطه مساحت قرار داده و مقدار آن را به دست می‌آوریم.

بنابراین خواهیم داشت:

 

 

در این مقاله به تشریح نحوه محاسبه مساحت و محیط مثلث متساوی‌الساقین پرداختیم و دیدیم که چگونه می‌توان با استفاده از اندازه ارتفاع و ساق‌های مثلث، اندازه قاعده آن را به دست آورد و بالعکس.

اگر شما نیز مثالی کاربردی در رابطه با این موضوع مد نظر دارید، آن را با ما و دیگر کاربران در میان بگذارید.