مقاله
نحوه محاسبه مساحت مخروط همراه با مثال های کاربردی
یکی از اشکال هندسی سه بعدی مخروط است که با برخی ویژگیها و تعریف آن در مطلب محاسبه حجم مخروط آشنا شدیم. در این مطلب قصد داریم تا با جزئیات بیشتری به تعریف مخروط پرداخته، با برخی ویژگیها و انواع مخروط آشنا شویم. در ادامه نحوه محاسبه مساحت مخروط را با استفاده از چند مثال کاربردی آموزش خواهیم داد.
با رایاد تا انتهای این مقاله همراه باشید.
مخروط و ویژگیهای آن
مخروط به یکی از گونههای هرم گفته میشود که قاعده آن دایرهای است. مخروطها اشکال هندسی ۳ بُعدی هستند که از سطح مقطع مخروط به آرامی یا به سرعت (بسته به سطح قاعده و ارتفاع مخروط) تا راس مخروط باریک میشوند.
در تعریف جزئیتر میتوان گفت که مخروط شکل هندسی سه بُعدی است که توسط یک صفحه پایه یا همان سطح مقطع مخروط محدود شده و سطح جانبی آن نیز مکان هندسی خطوط راستی هستند که نوک مخروط را به نقاط پیرامون سطح مقطع متصل میکنند.
توجه داشته باشید که هم رویه این شکل هندسی توپر و هم رویه پهلویی آن هر دو شکل هندسی مخروط به شمار میآیند.
ویژگی های مخروط
- راس مخروط همان نقطه انتهایی آن است.
- سطح مسطح مخروط قاعده آن نامیده میشود.
- مخروط دارای یک پایه مسطح است.
- مخروط دارای یک وجه منحنی شکل است.
- مخروط دارای یک سطح منحنی است و به همین دلیل چندوجهی محسوب نمیشود.
- مخروط نوعی مثلث است که از چرخاندن این مثلث تشکیل میشود.
- مثلث مذکور باید یک زاویه قائمه داشته باشد و حول یکی از دو ضلع کوتاهش یا همان ضلعهای غیر وتری چرخش داده شود.
- ضلع وتر مثلث حول محور مخروط میچرخد.
- در مخروط قائم فاصله همه نقاط روی قاعده دایرهای از رأس مخروط یکسان است.
- در مخروط قائم محور مخروط بر مركز قاعده عمود است.
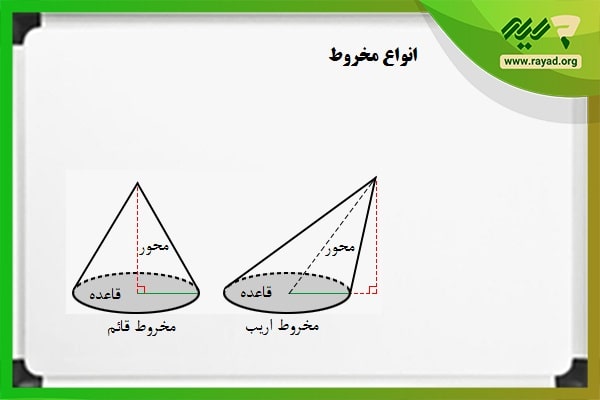
انواع مخروط
مخروطها دو نوع قائم یا اریب را شامل میشوند. مخروط قائم به مخروطی گفته میشود که محور آن روی مرکز قاعده عمود باشد. همچنین در این مخروط فاصله تمام نقاط روی قاعده از راس مخروط با همدیگر برابر است.
با وجود این، در مخروطهای اریب، محور مخروط روی مرکز قاعده عمود نیست و فاصله نقاط روی قاعده از راس مخروط با یکدیگر متفاوت است.
نکته مهم در مورد مخروطهای قائم و اریب این است که حجم یک مخروط اریب با مساحت قاعده معین و ارتفاعی مشخص میتواند با حجم مخروطی قائم با همان مساحت و ارتفاع معین برابر باشد.
مساحت مخروط
برای محاسبه مساحت مخروط باید مساحت جانبی مخروط را با مساحت قاعده آن جمع کنیم. در ابتدا نحوه محاسبه مساحت جانبی مخروط را بررسی میکنیم.
مساحت جانبی مخروط
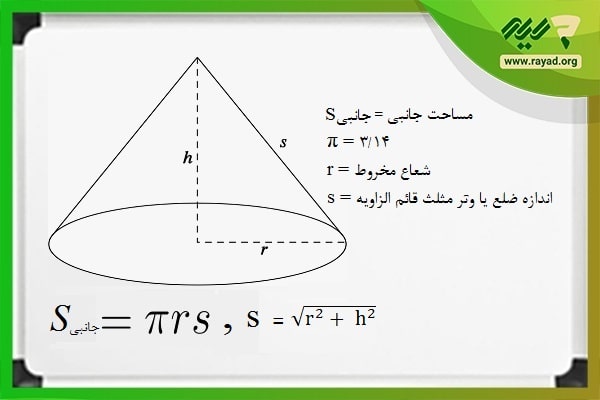
برای محاسبه اندازه سطح جانبی مخروط میتوانیم از فرمول زیر استفاده کنیم.
Sجانبی = π × r × s
در فرمول فوق، S نماد مساحت جانبی، π نماد عدد پی و معادل ۳/۱۴ بوده و r و s به ترتیب شعاع قاعده و طول ضلع مخروط هستند.
محاسبه اندازه ضلع مخروط
برای محاسبه s یا ضلع مخروط میتوانیم از رابطه فیثاغورس استفاده کنیم. در واقع، در مخروطهای فوق میبینیم که شعاع قاعده، محور و ضلع مخروط مثلثی قائم الزاویه را با هم تشکیل میدهند.
بنابراین با آگاهی از اندازه دو ضلع از این مثلث میتوان اندازه ضلع سوم را با رابطه فیثاغورس به دست آورد. با توجه به آن چه بیان کردیم، اندازه ضلع s در مخروطهای قائم با فرمول زیر به دست میآید: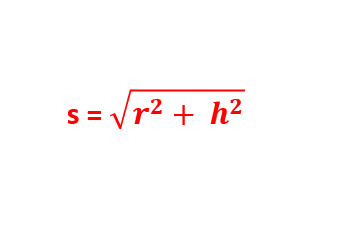
مساحت کل مخروط
همان طور که اشاره کردیم، مساحت کل مخروط از مجموع مساحت جانبی و مساحت قاعده آن به دست میآید.
پس از آشنایی با نحوه محاسبه مساحت جانبی مخروط، حال میتوانیم با محاسبه مساحت قاعده آن که یک دایره است، مساحت کل شکل را به دست آوریم.
از آنجایی که با نحوه محاسبه مساحت دایره آشنا هستیم، پس فرمول مساحت قاعده مخروط را به شرح زیر داریم:
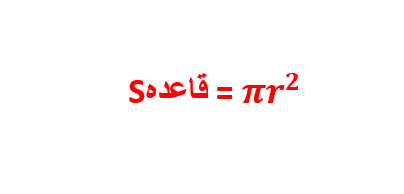
در فرمول فوق، A نماد مساحت کل مخروط، π نماد عدد پی و r و s به ترتیب شعاع قاعده و طول ضلع مخروط هستند. برای درک بهتر کاربرد این فرمول در ادامه چند مثال را حل میکنیم.
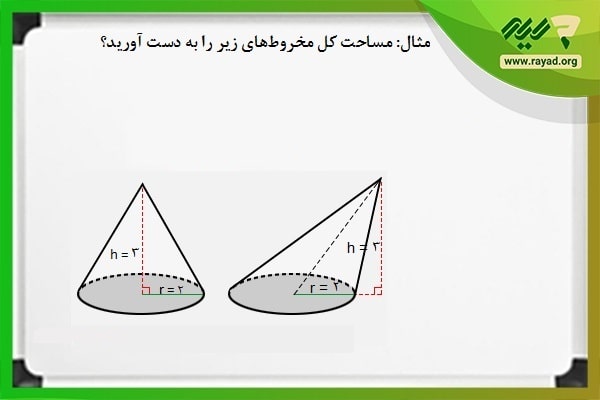
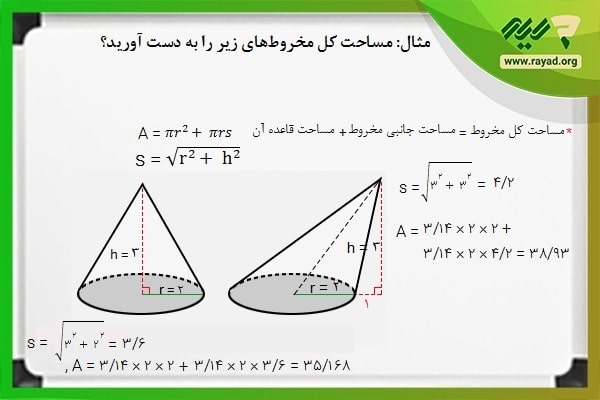
مثال: مساحت کل مخروطهای زیر را به دست آورید؟
برای محاسبه مساحت شکل هندسی مخروط، ابتدا مساحت قاعده مخروط ها و سپس اندازه مساحت جانبی آنها را محاسبه کرده و مقادیر را با هم جمع میکنیم.
همچنین برای محاسبه مقادیر s در هر دو مخروط میتوانیم با در دست داشتن اندازه دو ضلع مثلث قائم الزاویه، مقدار ضلع سوم را از رابطه فیثاغورس محاسبه کنیم. بنابراین خواهیم داشت:
مثال: فرض کنید کلاهی مخروطی شکل برای جشن تولد تهیه کردهایم. شعاع قاعده این کلاه ۸ سانتی متر و ارتفاع آن ۶ سانتی متر است. حال میخواهیم رویه این کلاه را با روکشی رنگی بپوشانیم. برای این کار به چند سانتی متر مربع کاغذ رنگی نیاز داریم؟
برای حل این مسئله باید بتوانیم مساحت جانبی مخروط را محاسبه کنیم.
همان طور که در این مطلب آموزش دادیم، با محاسبه اندازه ضلع مخروط از طریق رابطه فیثاغورس و جایگذاری مقادیر شعاع و اندازه ضلع در فرمول مساحت جانبی میتوانیم مقدار کاغذ رنگی مورد نیاز را به دست آوریم. بنابراین خواهیم داشت:
کلام آخر:
در این مقاله به مبحث مساحت مخروط و مثال کاربردی آن پرداختیم.اگر برای بدست آوردن مساحت دیگر اشکال هندسی نیازمند راه حل آسان هستید پیشنهاد رایاد به شما مطالعه مقاله مساحت و محیط اشکال هندسی است.

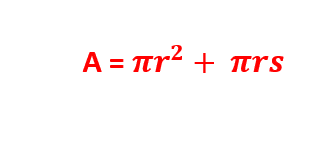


بسیارعالی ، ممنون