محیط و مساحت مثلث قائم الزاویه

مثلث قائم الزاویه یکی از انواع مثلث های پرکاربرد است که یکی از زاویه‌های آن قائمه یا ۹۰ درجه می‌باشد. این شکل هندسی زیرمجموعه مثلث‌ها بوده و تنها تفاوتش با مثلث ساده زاویه داخلی ۹۰ درجه آن است.

در مقاله محیط و مساحت مثلث ها با روش محاسبه انواع مثلث آشنا شدیم اما حال وقتش است جزیی تر به ایم شکل هندسی بنگریم و ضمن آشنایی با روش‌های محاسبه محیط و مساحت این مثلث، ویژگی‌های این شکل هندسی را هم بررسی می‌کنیم.

همچنین چند مثال کاربردی در رابطه با فرمول مثلث قائم‌الزاویه را بیان خواهیم کرد.

با رایاد همراه باشید.

 

 

ویژگی های مثلث قائم الزاویه

برخی از مهم‌ترین ویژگی‌های این مثلث موارد زیر را شامل می‌شوند:

• یکی از زوایای این مثلث برابر با ۹۰ درجه است.
• ضلع مقابل به زاویه ۹۰ درجه وتر مثلث قائم الزاویه نامیده می‌شود.
• طولانی‌ترین ضلع مثلث قائم الزاویه وتر آن است.
• مجموع دو زاویه داخلی دیگر در قائم الزاویه برابر با ۹۰ درجه است.
• اضلاع مجاور به زاویه قائمه قاعده و ارتفاع مثلث به شمار می‌آیند.

در ادامه روش محاسبه مساحت و محیط مثلث قائم الزاویه را آموزش می‌دهیم.

 

محیط مثلث قائم الزاویه

برای به دست آوردن محیط مثلث قائم الزاویه همچون سایر اشکال هندسی مثلثی، کافی است اندازه اضلاع آن را با همدیگر جمع کنیم. بنابراین خواهیم داشت:

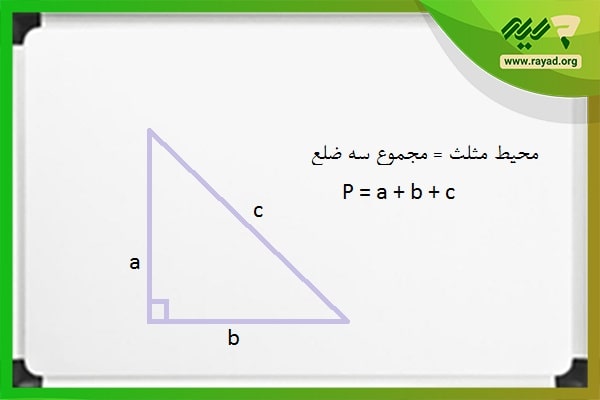
فرمول محیط مثلث قائم الزاویه = مجموع اندازه سه ضلع

 

این رابطه بر اساس فرمول‌های ریاضیاتی به صورت زیر خواهد بود:

P = a + b + c

در رابطه فوق P محیط مثلث بوده و a،‌ b و c به ترتیب ساق‌ها و وتر قائم الزاویه هستند.

 

 

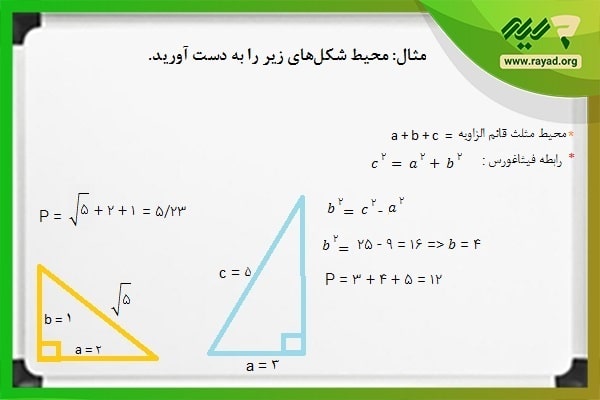
مثال: محیط شکل‌های زیر را به دست آورید.

 

 

همان طور که اشاره شد، برای به دست آوردن محیط شکل‌های فوق کافی است که اندازه هر سه ضلع را با هم جمع کنیم.

در مواردی هم که اندازه ضلعی را نمی‌دانیم، با استفاده از رابطه فیثاغورس می‌توانیم مقدار آن را محاسبه کنیم.

در مقاله انواع مثلث گفتیم که در رابطه فیثاغورس مربع اندازه وتر با مجموع مربعات اضلاع مجاور به زاویه قائمه برابر است. به عبارت دیگر داریم:

c^۲= a^۲+ b^۲

بنابراین برای شکل آبی ابتدا اندازه وتر را با رابطه فوق به دست آورده و سپس اندازه اضلاع آن را با هم جمع می‌کنیم. محیط مثلث دیگر نیز با جمع اضلاع آن قابل محاسبه است.

بنابراین خواهیم داشت:

 

برای آشنای با روش محاسبه مساحت و محیط اشکال هندسی روی آن کلیک کنید.

 

مساحت مثلث قائم الزاویه با وتر

مساحت این مثلث همچون سایر مثلث‌ها از فرمول قاعده ضرب در ارتفاع تقسیم بر دو به دست می‌آید.

همچنین با آگاهی از وتر مثلث و یکی از اضلاع زاویه قائمه آن می‌توان اندازه ضلع دیگر را به دست آورده، سپس مقادیر ارتفاع و قاعده را در رابطه مساحت قرار داده و اندازه مساحت شکل را به دست آورد.

بر این اساس خواهیم داشت:

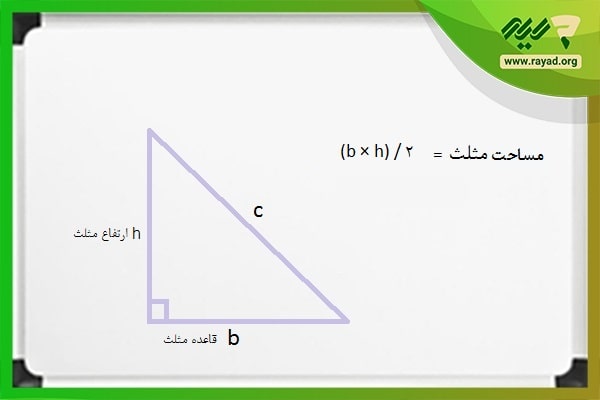
فرمول مساحت مثلث قائم الزاویه با وتر = (قاعده × ارتفاع) ÷ ۲

این رابطه با نمادهای ریاضیاتی به صورت زیر خواهد بود:

S = (b × h) ÷ 2

 

 

مثال: مساحت مثلث‌های قائم الزاویه زیر را به دست آورید.

 

 

برای محاسبه وتر مثلث آبی فوق، مشابه مثال قبل از رابطه فیثاغورس استفاده کرده و اندازه آن را به دست می‌آوریم.

سپس با قرار دادن مقادیر قاعده و ارتفاع هر مثلث در رابطه مساحت می‌توان اندازه سطح هر دو شکل را به دست آوریم. با این توضیحات داریم:

 

 

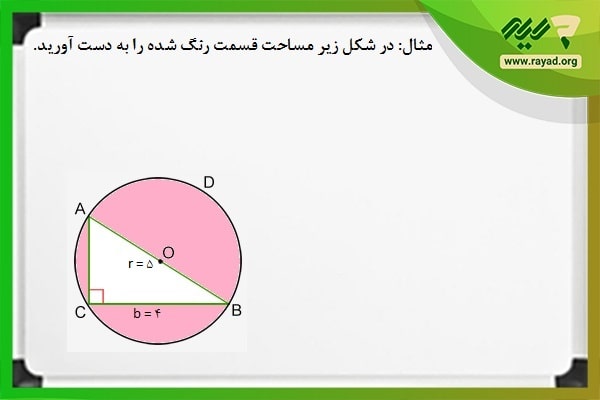
مثال: در شکل زیر مساحت قسمت رنگ شده را به دست آورید.

 

 

برای محاسبه اندازه سطح قسمت رنگی ابتدا باید مساحت دایره را به دست آورده، سپس مساحت مثلث را محاسبه کنیم و در آخر این دو مقدار را از هم کم کنیم.

همان طور که در شکل می‌بینید،‌ قطر دایره وتر قائم الزاویه را تشکیل می‌دهد.

همچنین برای محاسبه ضلع دیگر زاویه قائمه می‌توانیم از رابطه فیثاغورس استفاده کرده و به این ترتیب اندازه ارتفاع مثلث را به دست آوریم.

بنابراین محاسبات زیر را انجام می‌دهیم:

 

 

مثال: محدوده‌ای مستطیلی به ابعاد ۶ متر در ۸ متر داریم و می‌خواهیم کف آن را با کفپوش‌هایی به شکل مثلث قائم الزاویه بپوشانیم.

اضلاع زاویه قائمه این کفپوش‌ها به ترتیب ۳ و ۴ متر هستند. برای این کار به چند تا از این کفپوش‌ها نیاز خواهیم داشت؟

 

 

برای حل مسئله ابتدا باید بدانیم اندازه سطح محدوده مربعی چقدر است که برای این منظور به محاسبه مساحت مستطیل نیاز داریم.

سپس مساحت کفپوش‌ها را به دست آورده و در ادامه اندازه سطح کفپوش‌ها را بر اندازه سطح زمین مربعی تقسیم کنیم.

با این توضیحات مسئله را به صورت زیر حل می‌کنیم:

 

 

یادگیری ریاضی با استفاده از فیلم‌های آموزشی یکی از موثرترین روش‌های یادگیری این درس می‌باشد. اگر به دنبال فهم عمیق و تثبیت مباحث ریاضی در ذهن خود هستید، فیلم های آموزشی رهپویان پیشنهاد ما به شماست. در این مجموعه از فیلم‌های آموزشی تمامی محتوای کتاب ریاضی مربوط به هر پایه تحصیلی مطابق با سرفصل‌های کتاب درسی با جدیدترین متدهای آموزشی، تدریس می‌شود.

 

در این مقاله مساحت و محیط مثلث قائم الزاویه را با توجه به فرمول‌های کاربردی آن‌ها آموزش دادیم و دیدیم که چگونه می‌توان با آگاهی از اندازه وتر این مثلث‌ها ضلع دیگر آن‌ها را به دست آورده و محاسبات لازم را برایشان انجام داد.

امیدواریم که به خوبی این با محیط و مساحت این مثلث آشنا شده باشید، نظرات خودتان را حتما با ما درمیان بگذارید.