هیچ محصولی در سبد خرید نیست.
مقاله
چگونه محیط و مساحت لوزی را محاسبه کنیم؟ + مثال های متنوع
در مقالات قبلی در رابطه با نحوه محاسبه محیط و مساحت دایره، متوازی الاضلاع، مستطیل و مربع صحبت کردیم. حال در این مطلب تصمیم داریم به سراغ چهارضلعی دیگر یعنی لوزی برویم و بعد از بیان فرمول محیط و مساحت لوزی با چندین نمونه مثال ساده و کاربردی مسئله را به صورت کامل شرح دهیم.
اگر به دنبال تمامی فرمول های ریاضی مساحت و محیط ها هستید پیشنهاد میکنم مقاله محیط و مساحت اشکال هندسی را مطالعه کنید.
با تیم آموزشی رایاد همراه باشید.
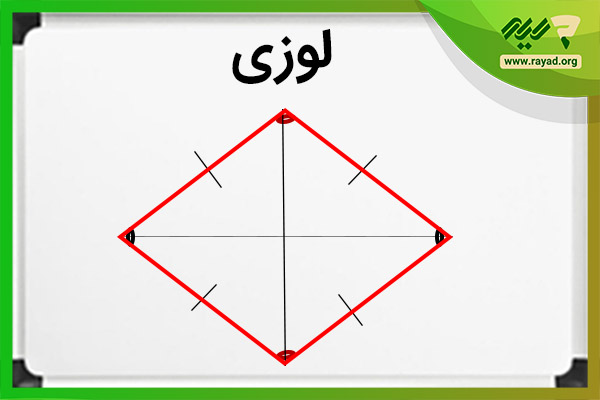
لوزی و خصوصیات آن
لوزی، یک نوع متوازی‌الاضلاع است که در آن طول اضلاع با هم برابر است، قطرها همدیگر را نصف می‌کنند، زاویه‌های روبرو با هم مساویند و ضلع‌های روبرو با هم موازیند.
ارتباط لوزی و مربع
اگرچه هردو چهارضلعی دو قطر دارند و در هردو، قطرها یکدیگر را نصف می‌کنند و عمود منصف یکدیگرند اما در مربع تمام اضلاع با هم برابرند و زاویه بین اضلاع 90 درجه است در صورتیکه در لوزی همیشه اینگونه نیست.
نکته: به طور کلی هرمربع یک لوزی است، زیرا تمام شرایط لوزی را دارد ولی عکس این قضیه صادق نیست.
فرمول مساحت لوزی
برای محاسبه مساحت لوزی کافیست از فرمول زیر کمک بگیرید.
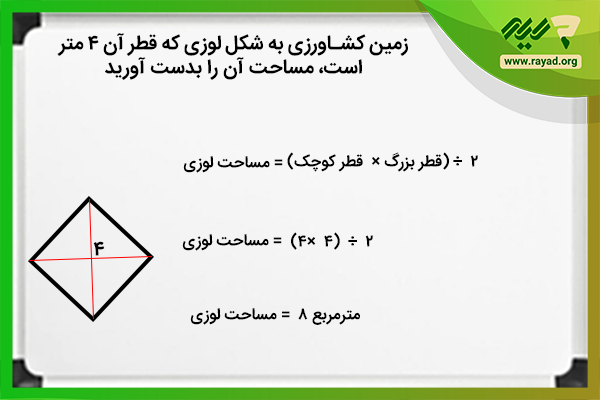
2 ÷ (قطر کوچک * قطر بزرگ) = مساحت لوزی
فرمول محیط لوزی
برای محاسبه محیط لوزی نیز باید از فرمول زیر استفاد کنید.
4 * یک ضلع = محیط لوزی
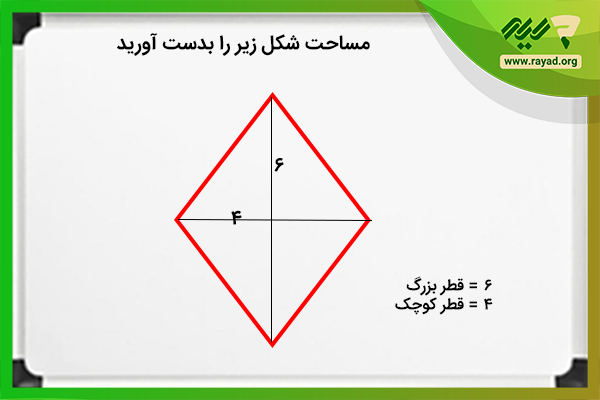
مثال ۱: مساحت شکل زیر را بدست آورید.
برای حل سوال تنها نیاز است فرمول مساحت لوزی را بنویسید و سپس جایگذاری کنید.
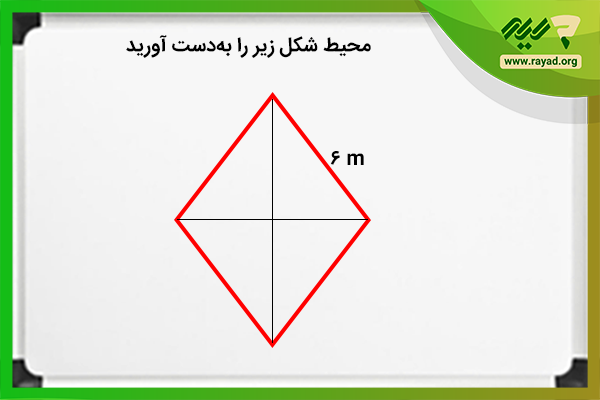
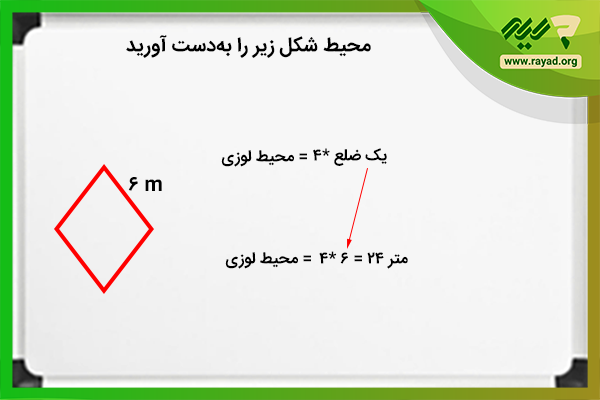
مثال ۲: اگر اندازه یکی از اضلاع لوزی ۶ متر باشد، محیط شکل چند متر است؟
برای حل این سوال نیز باید ابتدا فرمول محیط لوزی را بنویسید و سپس اندازه ضلع لوزی را در آن جایگذاری کنید.
جهت یادگیری موثر و مفهومی ریاضی می توانید در فرایند یادگیری از مجموعه فیلم های آموزشی رهپویان بهره مند شوید. برای دریافت اطلاعات بیشتر و خرید این مجموعه بر روی لینک فیلم های آموزشی رهپویان دانش و اندیشه کلیک کنید.
مثال ۳: می‌خواهیم دور تا دور فرش لوزی شکل مدرسه را با صندلی‌‌های کوچکی پر کنیم تا بتوانیم با بچه‌ها بازی کنیم، مدیر مدرسه بر این باورست که دور تا دور شکل (محیط) برابر با ۱۲ متر است، اندازه هر ضلع لوزی چند متر است؟
اگر به صورت سوال توجه کنید، متوجه میشوید که سوال محیط لوزی را داده و از ما اندازه ضلع را می‌خواهد. برای حل این سوال باید جدول ضرب را به خوبی حفظ کرده باشید تا در یافتن جواب به مشکل برنخورید.
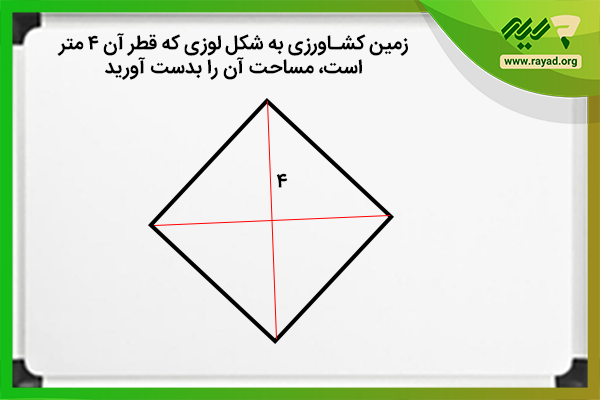
مثال ۴: یک زمین کشاورزی داریم که هر قطر آن برابر با ۴ متر است و می‌خواهیم در آن بذر گندم بکاریم، مساحت این زمین چند متر مربع است؟
برای حل سوال کافیست فرمول مساحت لوزی را بنویسید و سپس برای محاسبه فقط اعداد را جایگذاری کنید.
نکته مهم
مبحث مساحت و محیط اشکال هندسی یکی از مهم ترین مسئله های ریاضی می باشد که دانش آموزان برای نخستین مرتبه با این مفاهیم در مقطع دبستان آشنا می شوند. یادگیری مفهومی مساحت و محیط اشکال هندسی بسیار مهم است، چرا که یکی از پرکاربرد ترین مباحث نه تنها در ریاضی بلکه در زندگی می باشد.
آموزش صحیح و استمرار در حل تمرین و نمونه سوالات مفهومی این مبحث از طریق نرم افزار های آموزشی نیز ممکن است. از جمله نرم افزار آموزشی مناسب مقطع دبستان می توان سی دی های میشا و کوشا را نام برد، که از طریق بازی و آموزش غیر مستقیم مطالب درسی را آموزش می دهد.
فرمول محیط لوزی با قطر
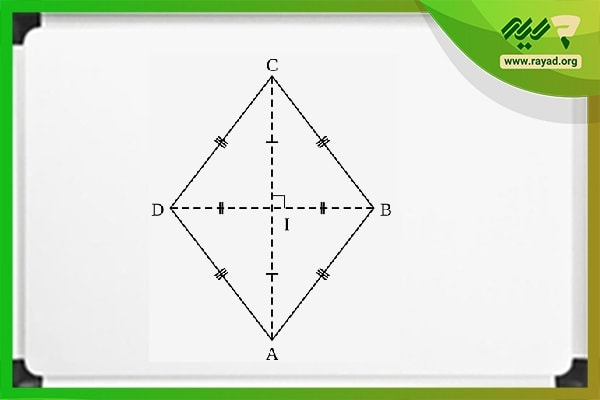
همان‌طور که اشاره شد، قطرها در لوزی عمود منصف یکدیگر هستند. از سوی دیگر، تقاطع آنها در لوزی چهار مثلث قائم‌الزاویه را به وجود می‌آورد. به شکل زیر توجه کنید:
بنابراین برای محاسبه محیط لوزی با قطر می‌توانیم ابتدا اندازه وتر یکی از چهار مثلث تشکیل‌شده را پیدا کرده و در ادامه آن را در عدد ۴ ضرب کنیم. توجه داشته باشید که در شکل فوق وتر یکی از مثلث‌ها در واقع یکی از اضلاع لوزی به شمار می‌آید.
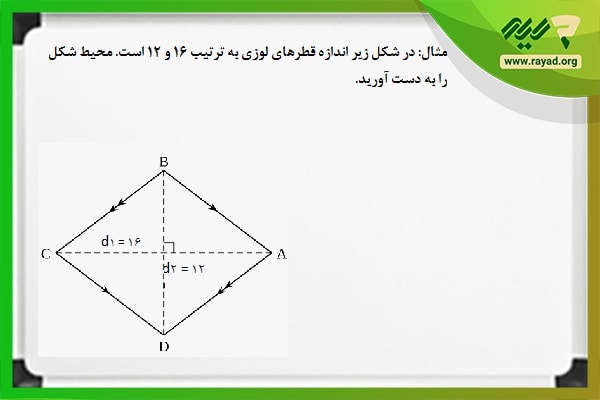
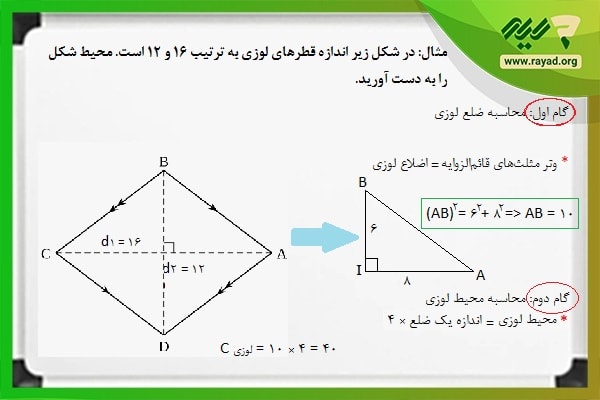
مثال 5: در شکل زیر اندازه قطرهای لوزی به ترتیب ۱۶ و ۱۲ است. محیط شکل را به دست آورید.
از آنجایی که قطرهای لوزی عمود منصف هم هستند، بنابراین داخل لوزی چهار مثلث قائم‌الزاویه داریم که اندازه اضلاع قائمه آنها به ترتیب ۶ و ۸ می‌باشند. حال اگر بخواهیم اندازه یکی از اضلاع شکل لوزی را به دست آوریم، می‌توانیم اندازه وتر یکی از مثلث‌های قائم‌الزاویه را محاسبه کنیم. بنابراین خواهیم داشت:
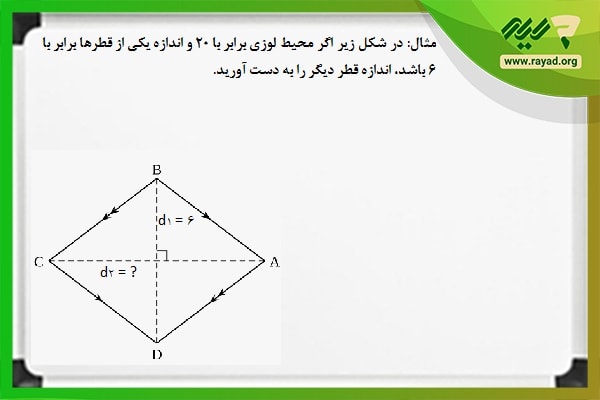
مثال 6: در شکل زیر اگر محیط لوزی برابر با ۲۰ و اندازه یکی از قطرها برابر با ۶ باشد، اندازه قطر دیگر را به دست آورید.
برای محاسبه اندازه قطر دوم لوزی بر اساس مراحل زیر عمل می‌کنیم:
- ابتدا اندازه ضلع آن را از روی مقدار محیط به دست می‌آوریم.
- به علاوه می‌دانیم که اضلاع لوزی به منزله وتری برای هر یک از چهار مثلث قائم‌الزاویه داخلی هستند. بنابراین با در دست داشتن اندازه وتر و یکی از اضلاع مثلث قائم‌الزاویه، می‌توانیم با رابطه فیثاغورث مقدار ضلع دوم را به دست آوریم.
- همچنین گفتیم که قطرها در لوزی همدیگر را نصف می‌کنند. به همین دلیل با ضرب کردن مقدار ضلع مثلث در عدد ۲ به اندازه قطر دوم لوزی دست پیدا می‌کنیم. با توجه به آنچه توضیح داده شد، داریم:
عالی