مقاله
انواع مثلثها و نحوه محاسبه محیط و مساحت آنها
در مقاله محاسبه محیط و مساحت مثلث به تفصیل در رابطه با تعریف مثلث، ویژگیهای شاخص آن و نحوه محاسبه محیط و مساحت مثلث صحبت کردیم. حال در این مقاله قصد داریم تا انواع مثلثها را بر اساس اندازه اضلاع و اندازه زاویههای داخل آنها معرفی کرده و نحوه محاسبه محیط و مساحت مثلث ها را مورد بررسی قرار دهیم.
اگر به دنبال تمامی فرمول های ریاضی مساحت و محیط ها هستید پیشنهاد میکنم مقاله محیط و مساحت اشکال هندسی را مطالعه کنید.
با تیم آموزشی رایاد همراه باشید.
انواع مثلث بر اساس اندازه اضلاع و زوایای آنها
به طور کلی، مثلثها بر اساس اندازه اضلاع آنها به دو دسته متساوی الاضلاع و متساوی الساقین تقسیم میشوند. همچنین بر اساس زوایای داخلی هم میتوان آنها را در سه دسته متساوی الاضلاع، متساوی الساقین و قائم الزاویه قرار داد.
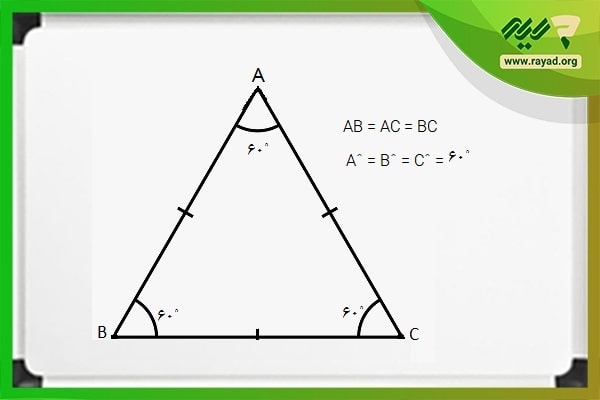
مثلث متساوی الاضلاع
مثلثی که تمامی اضلاع آن با هم برابر است، متساوی الاضلاع نامیده میشود. به علاوه، در این مثلثها اندازه هر یک از زوایای داخلی با هم برابر و معادل ۶۰ درجه هستند.
محاسبه محیط مثلث متساوی الاضلاع
در ابتدای مقاله اشاره کردیم که در برخی شرایط ممکن است در صورت سؤال به اندازه یک یا دو ضلع مثلث اشاره نشود. این در حالی است که برای پیدا کردن محیط یک مثلث به دانستن هر سه ضلع مثلث نیاز داریم. با وجود این، در مورد مثلثهای متساوی الاضلاع، اندازه هر سه ضلع با هم برابر است؛ پس به راحتی میتوان گفت که اندازه هر سه ضلع با همدیگر مساوی خواهد بود.
بر همین اساس، فرمول محاسبه دور تا دور مثلث متساوی الاضلاع برابر خواهد بود با:
اندازه یک ضلع × ۳ = محیط مثلث
مثال ۱: محیط مثلثهای متساوی الاضلاع زیر را به دست آورید.
از آنجایی که مثلثهای بالا هر دو متساوی الاضلاع هستند، پس اندازه هر سه ضلع آنها با هم برابر است. برای محاسبه اندازه دور تا دور آنها کافی است تا اندازه یکی از اضلاع را در عدد ۳ ضرب کنیم. پس خواهیم داشت:
نرم افزارهای آموزشی از جمله ابزارهای کمک آموزشی کارآمد هستند که زمینه را برای یادگیری مفهومی مطالب درسی فراهم می آورند. میشا و کوشا از جمله محصولات کمک آموزشی است که در یک فضای جذاب ریاضی را همراه با مثال های متعدد آموزش می دهد.
برای آشنایی بیشتر با این محصول بر روی لینک نرم افزار میشا و کوشا کلیک کنید.
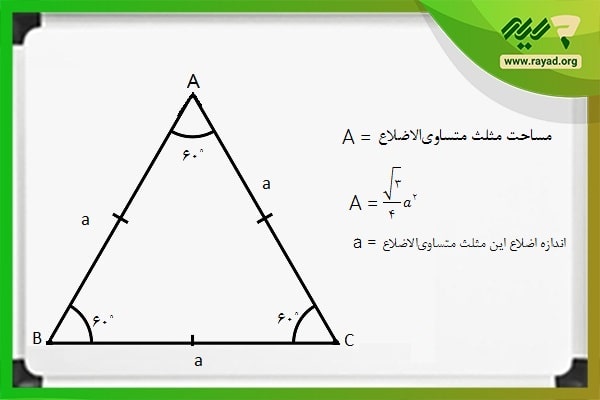
محاسبه مساحت مثلث متساوی الاضلاع
اگر فرض کنیم که اندازه هر یک از اضلاع این مثلث متساوی الاضلاع برابر با a باشد، مساحت این نوع مثلث از فرمول زیر به دست میآید:
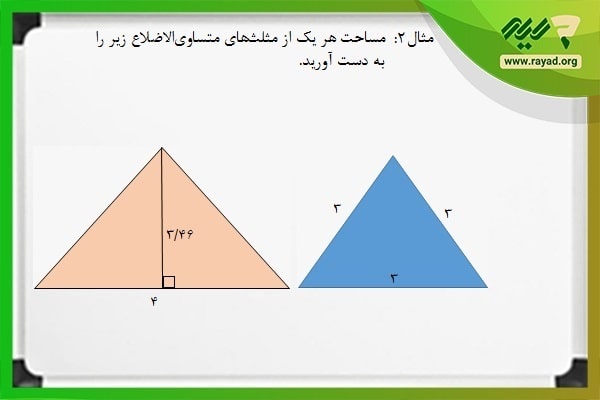
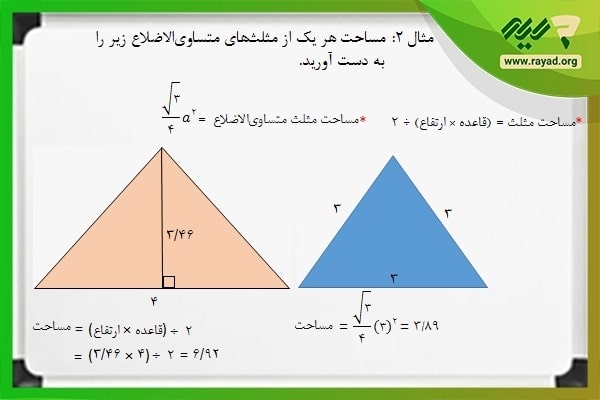
مثال ۲: مساحت هر یک از مثلثهای متساوی الاضلاع زیر را به دست آورید.
اگر بخواهیم از فرمول ارتفاع و قاعده برای محاسبه مساحت مثلث استفاده کنیم، باید اندازه قاعده و ارتفاع مثلث را در فرمول مربوطه جایگذاری کرده و حاصل را به دست آوریم. همچنین همانطور که اشاره کردیم، برای محاسبه اندازه سطح مثلثهای متساوی الاضلاع دانستن اندازه اضلاع نیز کفایت میکند. بر همین اساس خواهیم داشت:
مثلث متساوی الساقین
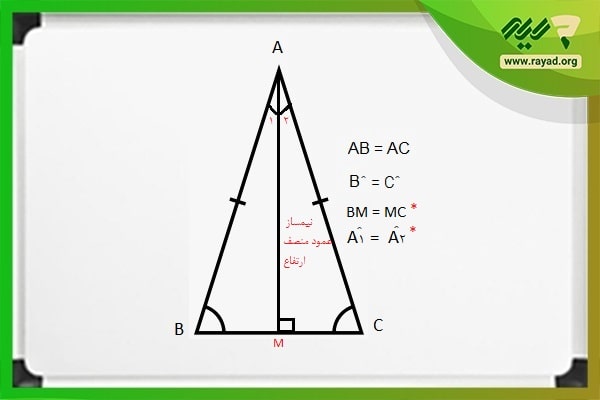
در مثلث متساوی الساقین دو ساق مثلث با هم برابر هستند و در آن علاوه دو ضلع برابر، دو زاویه برابر هم وجود دارد. در واقع، دو زاویهای از مثلث با هم برابر هستند که مجاور به اضلاع برابر بوده و روبهروی هم قرار میگیرند.
نکته ۱: مثلث متساوی الاضلاع نیز نوعی مثلث متساوی الساقین محسوب میشود.
نکته ۲: در مثلثهای متساوی الساقین نیمساز، عمود منصف و ارتفاع رسم شده از رأس A (رأس غیر مجاور به زاویههای برابر) بر هم منطبق هستند.
خب حالا که با محاسبه انواع مثلث ها آشنا شدید پیشنهاد میکنم یه سری به تور گرجستان لحظه آخر بزنید !
محاسبه محیط مثلث متساوی الساقین
برای محاسبه اندازه دور تا دور مثلث متساوی الساقین نیز همچون سایر مثلثها کافی است تا اندازه هر سه ضلع مثلث را با هم جمع کنید. همچنین ممکن است که در صورت سؤال اندازه یکی از اضلاع دو به دو برابر قید شود. در چنین شرایطی، از آنجایی که میدانیم دو ضلع روبهرو با هم برابر هستند، پس مشکلی در محاسبه محیط مثلث نخواهیم داشت.
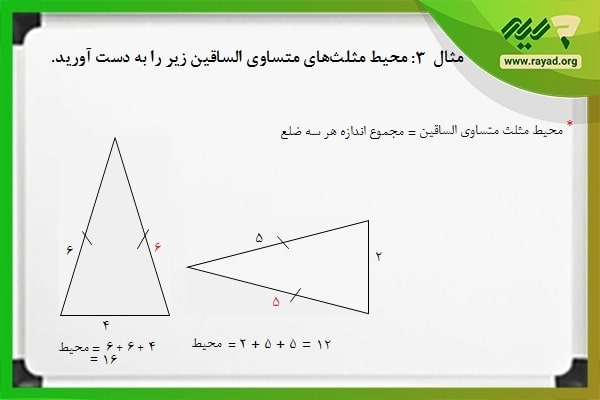
مثال ۳: محیط مثلثهای متساوی الساقین زیر را به دست آورید.
برای به دست آوردن اندازه دور تا دور هر یک از شکلهای فوق کافی است تا اندازه هر سه ضلع آنها را با هم جمع کنیم. پس خواهیم داشت:
مجموعه رهپویان دانش و اندیشه ارائه دهنده ی فیلم های آموزش مفهومی ریاضی در تمام مقاطع تحصیلی می باشد. جهت آشنایی با این مجموعه کارآمد تنها باید بر روی لینک رهپویان کلیک نمایید.
محاسبه مساحت مثلث متساوی الساقین
برای محاسبه اندازه سطح مثلثهای متساوی الساقین از همان رابطه رایج مساحت مثلث استفاده میکنیم. بنابراین فرمول محاسبه اندازه سطح مثلث متساوی الساقین به صورت زیر است:
۲ ÷ (قاعده × ارتفاع) = مساحت مثلث متساوی الساقین
مثال ۴: در شکل زیر مساحت مثلث متساوی الساقین را به دست آورید.
مثلث قائم الزاویه
مثلث قائم الزاویه یکی دیگر از زیرمجموعه اشکال هندسی مثلثی است که کاربرد بسیار زیادی در مسائل ریاضی دارد. تنها تفاوت این مثلث با دیگر مثلثها قائمه بودن یکی از زوایای داخل آن است. همچنین در این مثلثها با در دست داشتن اندازه دو ضلع میتوان به راحتی اندازه ضلع سوم را به دست آورد.
بر همین اساس در بسیاری از مسائل اندازه ارتفاع یا قاعده مثلث در صورت مسئله قید نمیشود. در حقیقت، برای محاسبه محیط یا مساحت مثلثهای قائم الزاویه، محاسبه یکی از دو مقدار ارتفاع یا قاعده مثلث به خود دانش آموزان واگذار میشود.
محاسبه محیط مثلث قائم الزاویه
برای محاسبه اندازه دور تا دور مثلث قائم الزاویه باید اندازه هر سه ضلع را با هم جمع کنیم. همانطور که پیشتر اشاره کردیم، در بسیاری از موارد تنها اندازه دو ضلع مثلث قائم الزاویه ذکر میشود و برای به دست آوردن اندازه ضلع سوم باید از رابطه فیثاغورس استفاده کنیم.
رابطه فیثاغورس در مثلثهای قائم الزاویه به صورت زیر است:
در رابطه بالا، a و b هر دو اضلاع مجاور به زاویه قائمه بوده و c ضلع روبهروی آن یا وتر مثلث است.
مثال ۵: محیط مثلث قائم الزاویه زیر را به دست آورید.
برای محاسبه اندازه دور تا دور مثلث باید ابتدا اندازه ضلع b را به دست آوریم که ارتفاع مثلث نیز به شمار میآید. بنابراین ابتدا از رابطه فیثاغورس استفاده کرده و ضلع b را به دست میآوریم و سپس اندازه هر سه ضلع را با هم جمع میکنیم. بر همین اساس خواهیم داشت:
محاسبه مساحت مثلث قائم الزاویه
برای محاسبه اندازه سطح مثلثهای قائم الزاویه نیز همچون سایر مثلثها از رابطه رایج مساحت مثلث استفاده میکنیم. در این مورد نیز ممکن است ابتدا ملزم به محاسبه اندازه قاعده یا ارتفاع مثلث قائم الزاویه بر اساس رابطه فیثاغورس باشیم.
بنابراین فرمول اندازه سطح مثلث قائم الزاویه به صورت زیر خواهد بود:
۲ ÷ (قاعده × ارتفاع) = مساحت مثلث قائم الزاویه
مثال ۶: مساحت مثلث قائم الزاویه زیر را محاسبه کنید.
برای محاسبه اندازه سطح مثلث بالا ابتدا باید اندازه قاعده آن را با استفاده از فرمول فیثاغورس به دست آورده و سپس عدد به دست آمده را در رابطه مساحت جایگذاری کنیم. پس خواهیم داشت:
مثلث مختلف الاضلاع:
یک نوع دیگر از مثلث، مثلث مختلف الاضلاع است. شاید نامش برای شما ترسناک باشد اما این مثلث بی آزارترین نوع است!
محیط مثلث مختلف الاضلاع:
فقط کافی است تمام اضلاع را باهم جمع ببنید:
اگر نام اضلاع ها a,b,c از فرمول زیر استفاده میکنیم:
a+b+c= محیط مثلث مختلف الاضلاع
مساحت مثلث مختلف الاضلاع:
مساحت مثلث مختلف الاضلاع همانند دیگر مثلث ها از رابطه ی زیر بدست می آید:
۲ ÷(قائده×ارتفاع)= مساحت مثلث مختلف الاضلاع
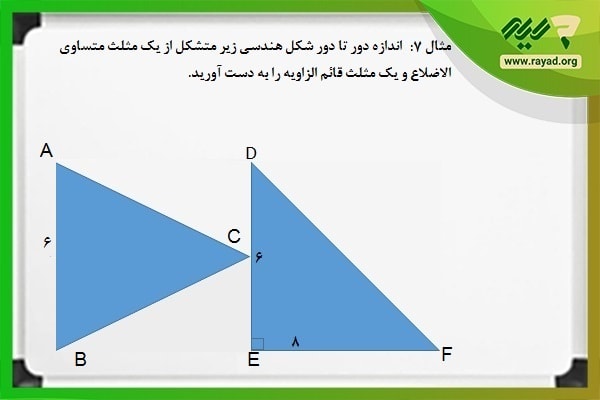
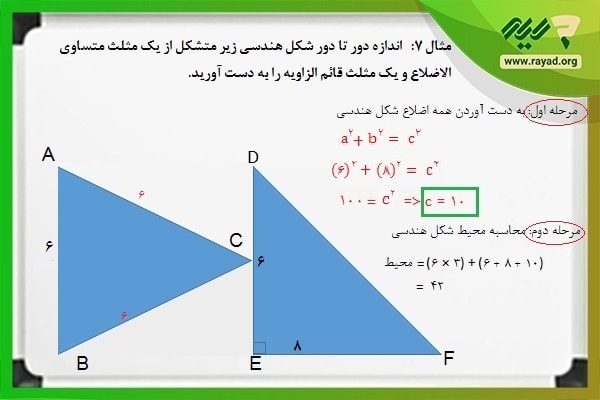
مثال ۷: اندازه دور تا دور شکل هندسی زیر متشکل از یک مثلث متساوی الاضلاع و یک مثلث قائم الزاویه را به دست آورید.
برای محاسبه اندازه دور تا دور شکل هندسی بالا ابتدا باید اندازه هر سه ضلع دو مثلث را به دست آورده، سپس محیط هر یک را محاسبه کرده و در نهایت آنها را با هم جمع کنیم. به علاوه، …
- از آنجایی که مثلث ABD متساوی الاضلاع است، تمامی اضلاع آن برابر با ۶ خواهند بود.
- مثلث EDF قائم الزاویه است و به همین دلیل ضلع سوم آن از رابطه فیثاغورس قابل محاسبه است.
بر همین اساس مراحل حل مسئله به صورت زیر خواهند بود:
قبل از اینکه به مثال بعدی مساحت مثلث بپردازیم یک زنگ تفریح کوتاه داشته باشیم. یک سری به اینجا تور گرجستان لحظه آخر بزنید.
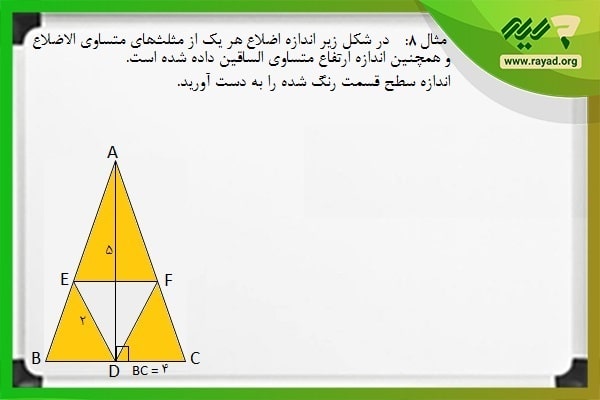
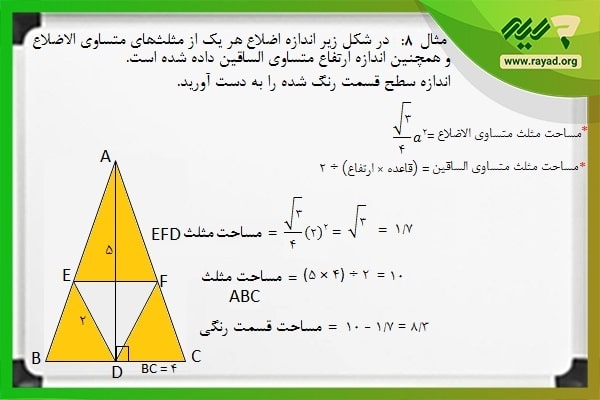
مثال ۸: در شکل زیر اندازه اضلاع هر یک از مثلثهای متساوی الاضلاع و همچنین اندازه ارتفاع متساوی الساقین داده شده است. اندازه سطح قسمت رنگ شده را به دست آورید.
بر اساس فرمول ارائه شده برای مساحت مثلثهای متساوی الاضلاع میتوانیم با در نظر گرفتن اندازه اضلاع مثلث معادل عدد ۲ و با در دست داشتن اندازه ارتفاع و قاعده مثلث متساوی الساقین، مساحت هر یک را به دست بیاوریم.
در ادامه اندازه سطح مثلث DEF را از مثلث ABC کم میکنیم تا اندازه سطح قسمت رنگ شده به دست آید. بنابراین خواهیم داشت:
نرم افزارهای آموزشی با فراهم کردن امکانات و فضای آموزشی مناسب فرایند یادگیری مفاهیم ریاضی و سایر دروس را برای دانش آموزان دبستانی آسان و جذاب نموده اند. جهت آشنایی با یکی از نرم افزارهای آموزشی ویژه دبستان بر روی لینک کیف آریا کلیک نمایید.



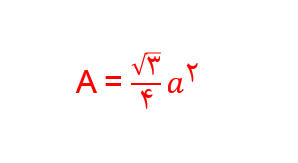

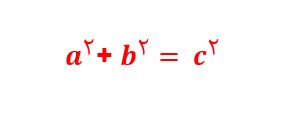





بد نبود
سپاس از توضیحات کاملتون.
عالی بود خیلی کمک میکنه