مقاله
آموزش محاسبه حجم مخروط + مثالهای کاربردی
مخروط یکی از گونههای هرم با قاعده دایرهای شکل است. در این مطلب قصد داریم تا ابتدا تعریفی جامع از مخروط ارائه داده، ویژگیهای مهم آن را نام برده و در ادامه نحوه محاسبه حجم مخروط را در قالب چند مثال کاربردی آموزش دهیم.
اگر به دنبال تمامی فرمول های ریاضی مساحت و محیط ها هستید پیشنهاد میکنم مقاله محیط و مساحت اشکال هندسی را مطالعه کنید.
با تیم آموزشی رایاد همراه باشید.
مخروط و ویژگیهای آن
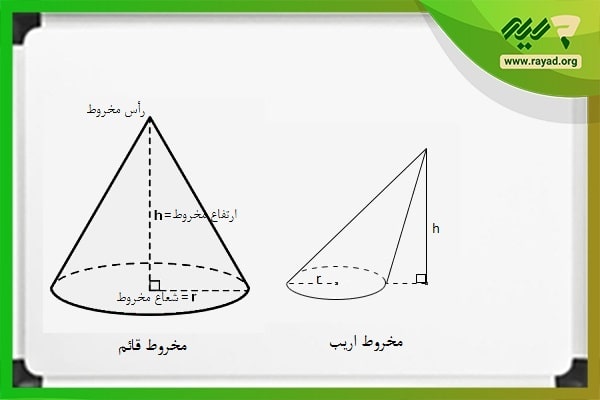
مخروط یک شکل هندسی سه بعدی است که از پایه تختش (سطح مقطع مخروط) به آرامی یا به سرعت (بسته به سطح قاعده و ارتفاع آن) تا رأس باریک میشود. به عبارت دیگر، شکل هندسی مخروط به صفحه پایه خود محدود شده و از به هم پیوستن خطوط راستی تشکیل شده است که رأس مخروط را به نقاط پیرامون پایه وصل میکنند.
از جمله مهمترین ویژگیهای مخروط میتوان به موارد زیر اشاره کرد:
- مخروط دارای یک پایه مسطح است.
- مخروط دارای یک وجه منحنی شکل است.
- از آنجایی که مخروط دارای یک سطح منحنی است، پس چندوجهی نیست.
- در مخروط قائم فاصله همه نقاط روی قاعده دایرهای از رأس مخروط یکسان است.
- در مخروط قائم محور مخروط بر مركز قاعده عمود است.
نکته: شکل هندسی مخروط هم به صورت قائم و هم به صورت اریب به کار گرفته میشود. همچنین حجم مخروطهای اریب و قائم با مساحت سطح مقطع و ارتفاع یکسان با همدیگر برابر است.
محاسبه حجم مخروط
برای به دست آوردن حجم مخروط باید مساحت سطح قاعده دایرهای آن را محاسبه کرده و آن را در اندازه ارتفاع ضرب کنیم. سپس مقدار حاصل را بر عدد ۳ تقسیم کنیم تا اندازه حجم مخروط به دست آید. بنابراین فرمول محاسبه حجم برای شکل هندسی مخروط به شرح زیر است:
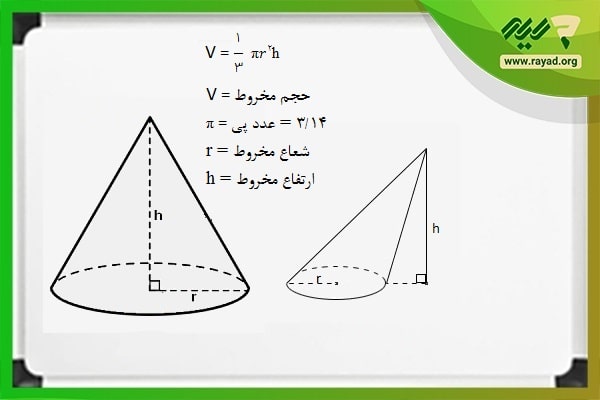
این رابطه بر اساس نمادهای ریاضیاتی به شرح زیر خواهد بود:
توجه داشته باشید که در رابطه فوق، V نماد حجم بوده، r و h به ترتیب شعاع استوانه و ارتفاع آن را نشان میدهند.
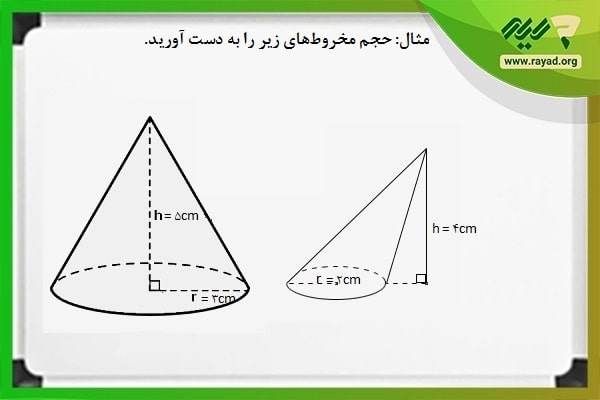
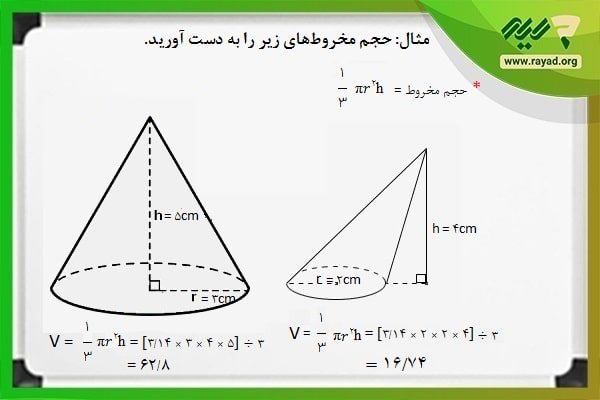
مثال: حجم مخروط های زیر را به دست آورید.
برای محاسبه حجم مخروط مساحت دایره را در قاعدههای هر دو شکل به دست آورده و سپس آن را در ارتفاع هر شکل ضرب کرده و در نهایت مقدار حاصل را بر عدد ۳ تقسیم میکنیم. پس خواهیم داشت:
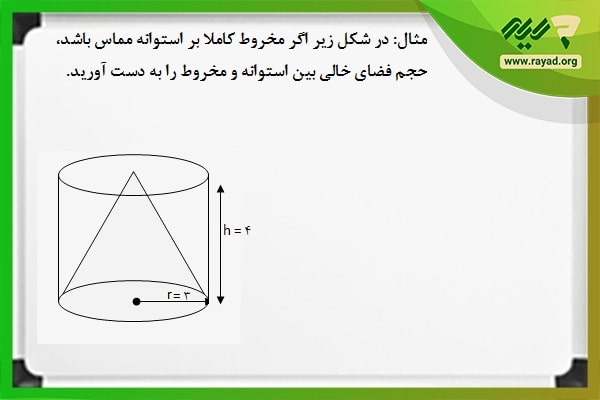
مثال: در شکل زیر اگر مخروط کاملاً بر استوانه مماس باشد، حجم فضای خالی بین استوانه و مخروط را به دست آورید.
از آنجایی که مخروط کاملاً بر استوانه مماس است، میتوان گفت که شعاع استوانه برابر با شعاع مخروط و ارتفاع دو شکل نیز با هم برابر است. حال برای محاسبه حجم فضای خالی بین این دو شکل کافی است ابتدا حجم استوانه را به دست آورده، سپس حجم مخروط را محاسبه کنیم و در آخر آنها را از هم کم کنیم. بنابراین خواهیم داشت:
مثال: فرض کنید میخواهیم یک عدد بستنی قیفی درست کنیم. اگر نان این بستنی مخروطی به شعاع ۴ سانتی متر و ارتفاع ۸ سانتی متر باشد، گنجایش بستنی آن را به دست آورید.
برای اینکه ببینیم این نان بستنی ظرفیت گنجایش چه مقدار بستنی را دارد، باید حجم آن را به دست آوریم. بنابراین از فرمول محاسبه حجم مخروط استفاده کرده و مقادیر شعاع و ارتفاع را در آن جایگذاری میکنیم. پس خواهیم داشت:
در این مقاله به چگونگی محاسبه حجم مخروط همراه با مثال پرداختیم. پیشنهاد رایاد به شما مطالعه ی مطلب مساحت مخروط نیز می باشد.


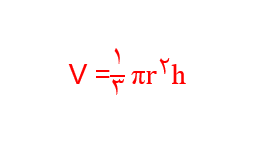



ممنون از این نوشته ها اگه نبود نمیتونستم تکالیفم را انجام بدم 😅💃❤️💋
خیلی عالی بود ممنون
سلام دوست عزیز
ممنون از توجه شما
سلام خسته نباشید عالی بودید
بسیار با مفهوم توضیح داده بودید
سلام دوست عزیز
خوشحالیم که محتوای آموزشی سایت رایاد برای شما مفید واقع شده.
سلام
چرا برای بدست اوردن حجم مخروط باید در اخر تقسیم بر سه کرد رابطش که و مساوی با یک سوم پی R به توان ۲ است
مثلا تو بالا نوشته
V=[یک سوم×پی×۳به توان دو×۴ ]÷۳
اینجا چرا تو اخر تقسیم بر سه شده
میشه تقسیم نکنی اول که 1/3 مینویسی همونجا با عدد پی ساده کنی که راه حل خوبی ولی در صورتی جواب میده که عدد پی رو ۳ در نظر بگیریم
زیرا در اصل فرمول حجم استوانه ای را محاسبه میکند که مخروط درون اوست. و در استوانه مورد سه مخروط هم حجم قرار میگیرد و چون ما حجم یک مخروط را میخواهیم تقسیم بر سه انجام میشود .