مقاله
محاسبه مساحت هرم با مثالهای کاربردی
هرمها اشکال هندسی هستند که در هندسه و فیزیک کاربردهای زیادی دارند. در این مقاله قصد داریم همراه با مثال های کاربردی چگونگی محاسبه ی مساحت هرم را توضیح دهیم.
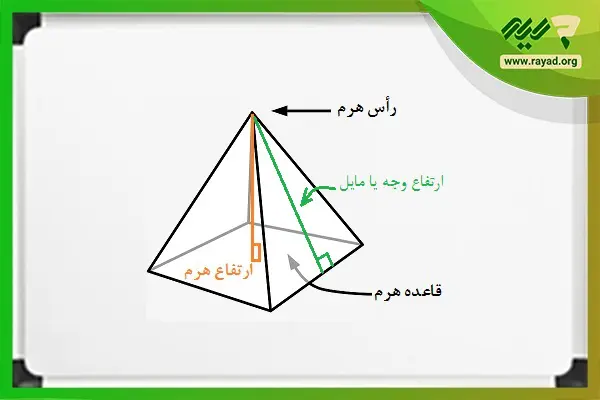
اتصال نقطهای در فضا با تمام نقاط شکلی بسته در صفحه موجب شکل گیری هرم میشود؛ این نقطه راس هرم نام دارد و شکل بسته مسطح نیز به عنوان قاعده هرم شناخته میشود.
در هرمها قاعده به صورت چند ضلعی دلخواه است. سایر وجهها در هرم مثلثهای هم راس هستند که در راسی مشترک به همدیگر متصل میشوند. ارتفاع هرم خط قائمی است که راس هرم را به قاعده آن متصل کرده و بر آن عمود میشود.
اگر به دنبال تمامی فرمول های ریاضی مساحت و محیط ها هستید پیشنهاد میکنم مقاله مساحت و محیط اشکال هندسی را مطالعه کنید.
با رایاد تا انتهای این مقاله همراه باشید.
ویژگیهای هرم
- هرمها اشکال هندسی چند وجهی هستند.
- چهار وجه هرم مثلثی است.
- وجه دیگر یا قاعده هرم معمولا مربع یا مستطیل است.
- ارتفاع هرم خطی است از راس هرم تا قاعده آن که بر سطح قاعده نیز عمود است.
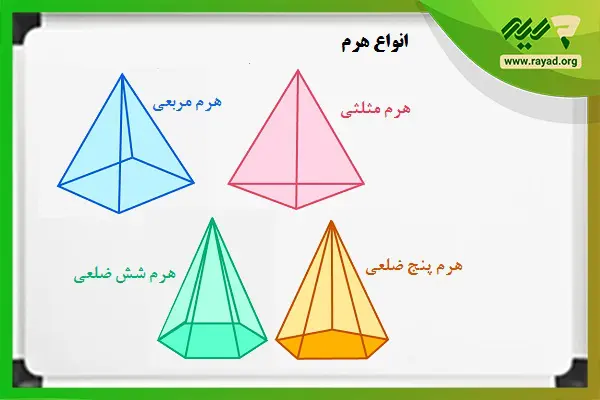
انواع هرم
هرمها بسته به سطح قاعدهشان میتوانند انواع مختلفی داشته باشند. البته لازم به ذکر است که هرمهای دارای قاعده مربع یا مستطیل کاربردهای بیشتری در هندسه و ریاضیات دارند. در ادامه انواع هرمها را آوردهایم.
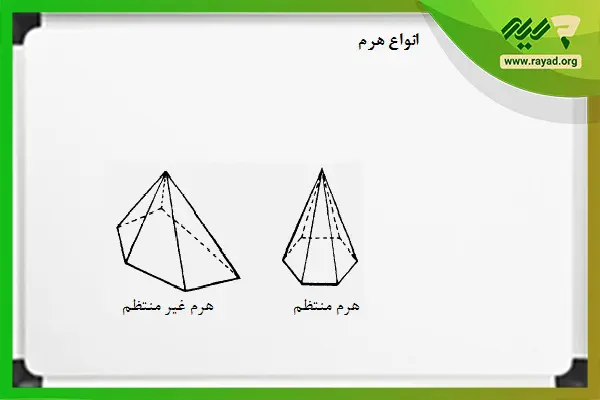
علاوه بر این، هرمها را میتوان در دو دسته کلی هرمهای منتظم و غیر منتظم نیز تقسیم بندی کرد. به عبارتی، اگر قاعده هرم یک چند ضلعی منتظم باشد، هرم را منتظم مینامیم و در غیر این صورت شکل ما در گروه هرمهای نامنتظم جای میگیرد.
نحوه محاسبه مساحت هرم منتظم
در هرمهای منتظم، همه وجههای جانبی هرم مثلثهای با ابعاد یکسان هستند. به همین دلیل برای محاسبه مساحت هرم میتوانیم از فرمول زیر استفاده کنیم:
مساحت هرم = مساحت قاعده + ۱/۲ × (محیط قاعده × طول مایل)
در اینجا منظور از مایل، ارتفاع یکی از وجوه هرم یا به عبارتی ارتفاع یکی از مثلثهای مربوطه به وجوه هرم میباشد. فرمول فوق بر اساس نمادهای ریاضیاتی به صورت زیر در میآید:
S = A + ۱/۲ (P × hl)
در این فرمول S نماد مساحت هرم، A مساحت قاعده هرم، P محیط قاعده و hl نیز ارتفاع وجه مثلثی هرم میباشد.
مساحت هرم نامنتظم
هرمهای نامنتظم وجوه جانبی با یکدیگر متفاوت هستند. به همین دلیل برای پیدا کردن مساحت هرم نامنتظم باید از فرمول زیر استفاده کنیم:
مساحت هرم = مساحت قاعده + مساحت جانبی
این رابطه بر اساس نمادهای ریاضیاتی به صورت زیر خواهد بود:
S = A + Sجانبی
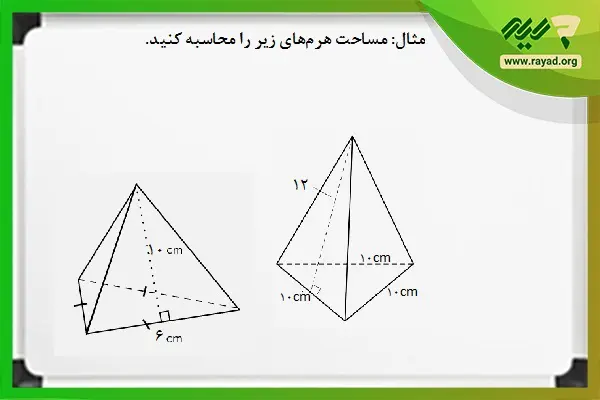
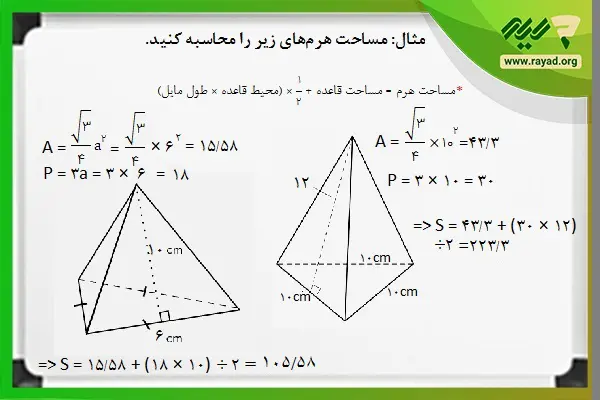
مثال: مساحت هرمهای زیر را محاسبه کنید.
برای محاسبه مساحت هرمها ابتدا باید مساحت قاعده آنها را به دست آوریم. مساحت مثلث متساوی الساقین به صورت زیر می باشد. برای آشنایی با مثال های بیشتر بر روی مطلب مساحت مثلث متساوی الساقین کلیک نمایید.
بنابراین با استفاده از این رابطه مساحت قاعده را به دست میآوریم. همچنین در مقاله انواع مثلث نیز گفتیم که محیط مثلث از مجموع اندازه سه ضلع آن به دست میآید.
با این راه کار نیز میتوانیم محیط قاعده را به دست آورده و با وارد کردن مقادیر مورد نظر در فرمول مساحت هرم، اندازه سطح دو شکل را به دست آوریم. با این توضیحات خواهیم داشت:
مثال: اگر بخواهیم با استفاده از مقواهای رنگی هرمی مربعی به طول ضلع ۵ سانتی متر، ارتفاع وجه مثلث معادل ۱۰ سانتی متر بسازیم، اندازه سطح این هرم چقدر خواهد بود؟
برای به دست آوردن اندازه سطح کافی است که مساحت هرم را به دست آوریم. بنابراین خواهیم داشت:
کلام آخر
در این مقاله به آموزش محاسبه مساحت هرم پرداختیم و شکل آن را دیدیم، در جهان ما اشکال زیادی شبیه به هرم ها هستند مثال آن اهرام ثلاثه مصر، شما دیگر چه چیز هایی شبیه به هرم ها دیده اید؟ برای ما در قسمت نظرات بنویسید.

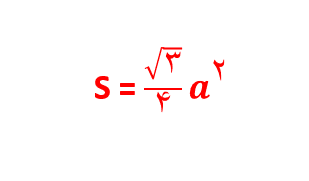

بالاخره مساحت چقد شد ؟؟؟