مقاله
محاسبه محیط و مساحت مثلث همراه با مثالهای کاربردی
از جمله اشکال هندسی پرکاربرد در مسائل مختلف ریاضی و هندسه میتوان به مثلثها اشاره کرد. مثلثها در حالت کلی از برخورد سه خط غیر هم راستا در صفحه به وجود میآیند که بر اساس اندازه اضلاع آنها انواع مختلفی را شامل میشوند. در این مقاله قصد داریم تا تعریفی کلی از مثلث ارائه داده و در ادامه نحوه محاسبه محیط و مساحت مثلث بر اساس انواع مختلف آن را در قالب مثالهایی کاربردی، ساده و قابل درک ارائه دهیم.
اگر به دنبال تمامی فرمول های ریاضی مساحت و محیط ها هستید پیشنهاد میکنم مقاله محیط و مساحت اشکال هندسی را مطالعه کنید.
با تیم آموزشی رایاد همراه باشید
مثلث
مثلث یا سهگوش یک چندضلعی مسطح با سه ضلع است که از اتصال سه خط غیر هم راستا در صفحه و در سه نقطه متمایز به وجود میآید. به طور کلی، هر مثلث دارای سه ضلع، سه زاویه و سه رأس است. به عبارت بهتر، یک مثلث از برخورد سه خط به وجود میآید که به صورت دو به دو همدیگر را در یک صفحه مسطح قطع میکنند. هر مثلث در حالت کلی ویژگیهای زیر را دارا است:
- مجموع زاویههای داخلی مثلث برابر با ۱۸۰ درجه است.
- مجموع زوایای خارجی در هر مثلث برابر با ۳۶۰ درجه است.
- در هر مثلث اندازه یک زاویه خارجی برابر با مجموع دو زاویه داخلی غیر مجاور آن است.
- هر مثلث ممکن است دو یا سه ضلع هماندازه داشته باشد یا هیچ ضلع برابری نداشته باشد.
- هر مثلث ممکن است دو یا سه زاویه برابر داشته باشد یا هیچ زاویه برابری نداشته باشد.
- هر مثلث دارای ۳ ارتفاع است که به عنوان پارهخطی از رأس مثلث به ضلع مقابل آن عمود میشوند.
- هر مثلث دارای ۳ نیمساز داخلی و ۳ نیمساز خارجی است که از هر رأس مثلث گذشته و آن را به دو زاویه مساوی تقسیم میکنند.
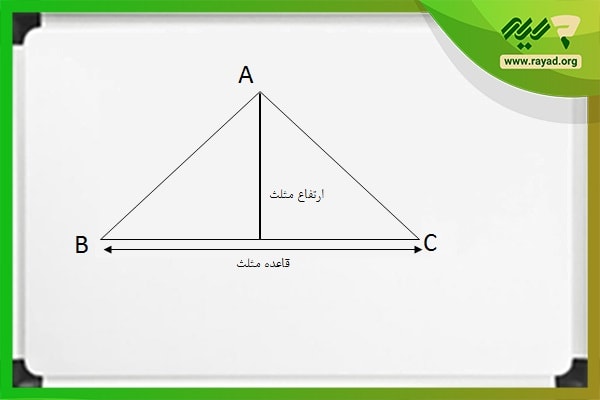
محیط مثلث
برای محاسبه محیط یک مثلث کافی است تا اندازه اضلاع آن را با هم جمع کنیم. بنابراین رابطه محیط مثلث برابر است با:
مجموع اندازه اضلاع = محیط مثلث
این فرمول بر اساس نمادهای ریاضیاتی به صورت زیر خواهد بود:
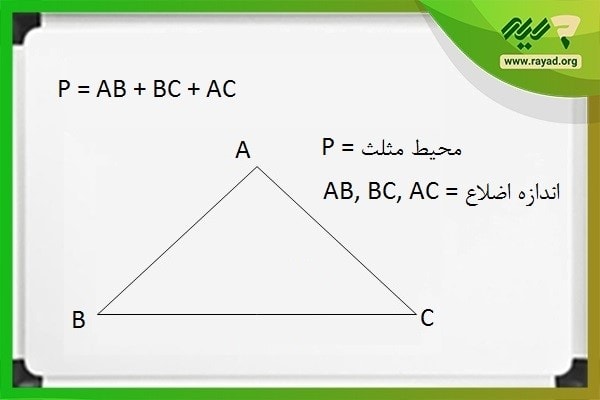
P = AB + BC + AC
توجه داشته باشید که در فرمول بالا، P نماد محیط مثلث است و هر یک از نمادهای AB، BC و AC به ترتیب اندازه هر یک از اضلاع مثلث هستند.
نکته: در برخی شرایط ممکن است که اندازه یک یا دو ضلع از مثلث را نداشته باشیم. این حالت را در مقاله معرفی انواع مثلثها و نحوه محاسبه محیط و مساحت آنها بررسی میکنیم.
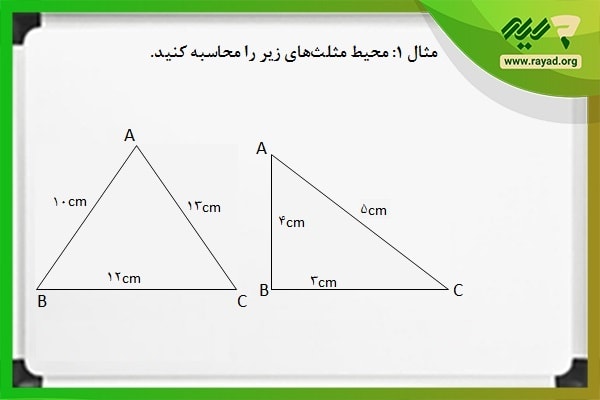
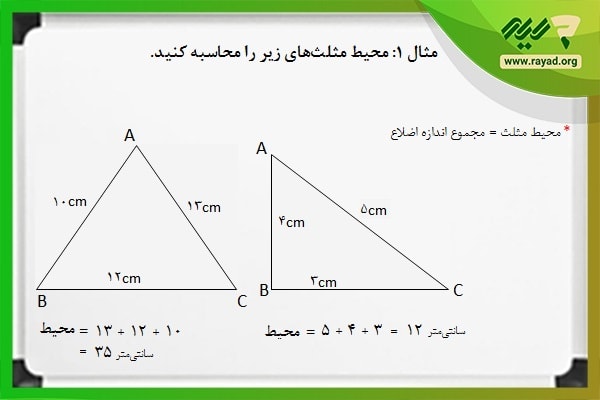
مثال ۱: محیط مثلثهای زیر را محاسبه کنید.
برای محاسبه اندازه دور تا دور هر یک از مثلثهای بالا باید ابتدا فرمول را نوشته و سپس اعداد مربوط به اندازه هر ضلع از مثلث را در آن جایگذاری کنیم. بنابراین خواهیم داشت:
مثال ۲: محیط اشکال هندسی زیر را محاسبه کنید.
برای محاسبه محیط شکل هندسی بالا باید ابتدا محیط مثلث، محیط مربع و محیط مستطیل را محاسبه کرده و سپس آنها را با هم جمع کنیم. بنابراین برای محاسبه دور تا دور شکل خواهیم داشت:
در مرحله بعد باید محیط هر سه شکل را با همدیگر جمع کنیم تا اندازه دور تا دور شکل هندسی به دست آید:
مثال ۳: فرض کنید یک میز سهگوش با اندازه اضلاع ۳۰، ۴۵ و ۵۵ سانتیمتر داریم که میخواهیم دور تا دور آن را با نوار نازک چوبی دورگیری کنیم. برای این کار به چند سانتیمتر نوار چوبی نیاز داریم؟
برای محاسبه مقدار نوار چوبی مورد نیاز، باید اندازه دور تا دور میز مثلثی یا محیط آن را محاسبه کنیم. بنابراین خواهیم داشت:
محاسبه مساحت مثلث
مساحت هر مثلث با اندازه سطح آن برابر است و برای محاسبه آن نیاز به اندازه قاعده، اندازه ارتفاع و در برخی موارد به اندازه محیط مثلث نیاز داریم. در حقیقت، دو روش برای محاسبه اندازه سطح مثلث وجود دارد که عبارتند از:
- استفاده از فرمول قائده و ارتفاع مساحت مثلث
- استفاده از فرمول هرون
فرمول مساحت مثلث با استفاده از قائده و ارتفاع
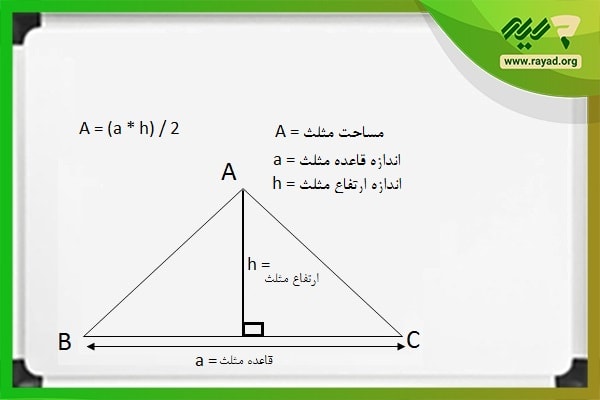
یکی از سادهترین راههای محاسبه اندازه سطح مثلث استفاده از فرمول مساحت است. فرمول محاسبه سطح در شکلهای مثلثی برابر است با:
۲ ÷ (قاعده × ارتفاع) = مساحت مثلث
این فرمول بر اساس نمادهای ریاضی به صورت زیر خواهد بود:
A = (a * h) / 2
در رابطه بالا A نماد مساحت، a اندازه قاعده مثلث و h اندازه ارتفاع آن است.
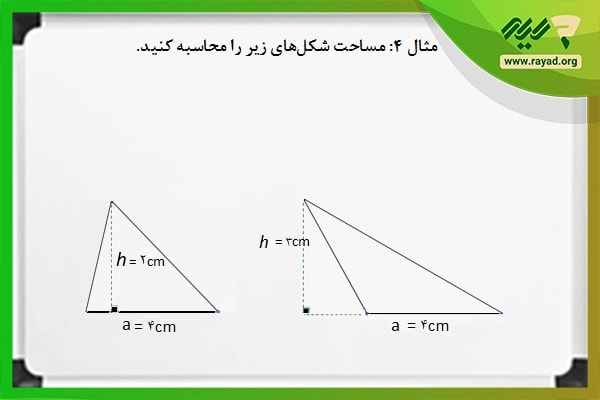
مثال ۴: مساحت شکلهای زیر را محاسبه کنید.
برای محاسبه اندازه سطح هر یک از مثلثهای بالا اندازه قاعده و ارتفاع آنها را در فرمول مساحت جایگذاری میکنیم. پس خواهیم داشت:
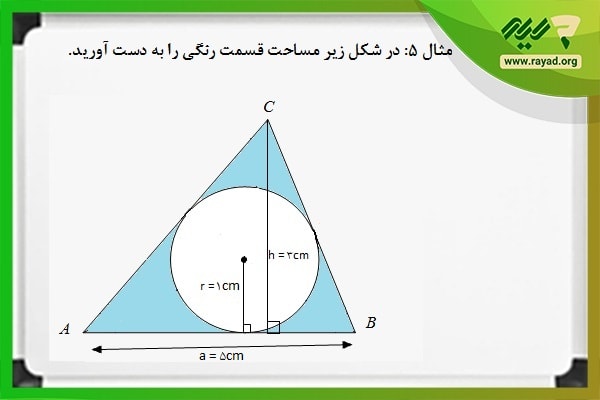
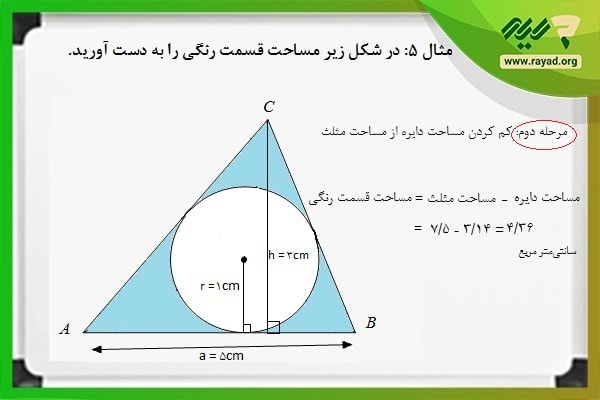
مثال ۵: در شکل زیر اندازه سطح قسمت رنگی را به دست آورید.
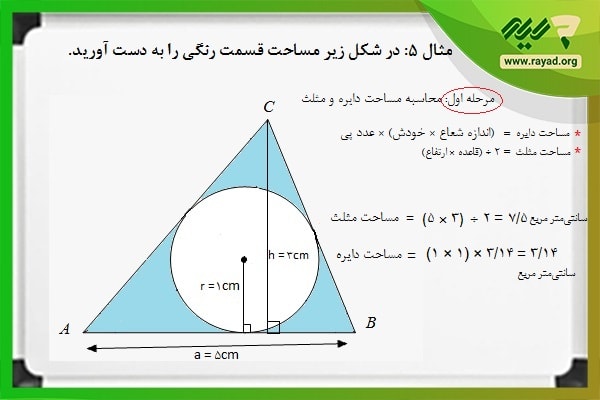
برای به دست آوردن اندازه سطح قسمت رنگشده لازم است در ابتدا مساحت دایره و مساحت مثلث را محاسبه کرده و سپس آنها را از هم کم کنیم. پس خواهیم داشت:
در مرحله دوم اندازه سطح دایره را از اندازه سطح مثلث کم میکنیم تا مساحت قسمت رنگی به دست آید. بنابراین داریم:
مثال ۶: فرض کنید میزی سهگوش با اندازه اضلاع ۳۰، ۴۵ و ۵۵ سانتیمتر داریم. اگر بخواهیم روکشی پلاستیکی برای این میز تهیه کنیم، به چند سانتیمتر مربع روکش نیاز خواهیم داشت؟
برای محاسبه اندازه روکش مورد نیاز باید اندازه سطح میز مثلثی را محاسبه کنیم. بنابراین با استفاده از فرمول خواهیم داشت:
محاسبه مساحت مثلث با استفاده از فرمول هرون
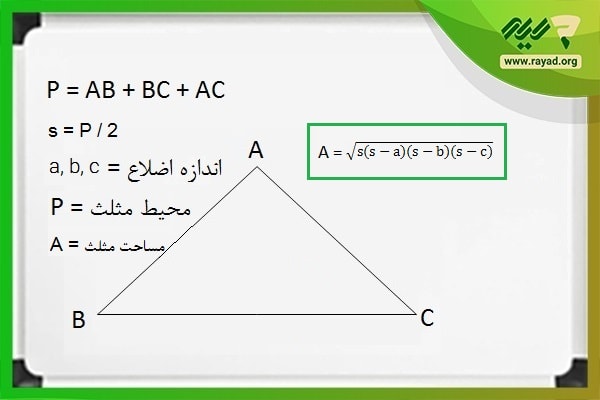
در برخی شرایط خاص، ممکن است صورت سؤال محیط مثلث را داده و در ادامه محاسبه مساحت آن را از ما بخواهد. حال اگر ارتفاع مثلث یا قاعده آن را نداشته باشیم، در این صورت با استفاده از فرمول هرون میتوانیم مساحت مثلث را بیایم. بر اساس فرمول هرون، مساحت یک مثلث با اضلاعی به طول a، b و c را میتوان از رابطه زیر محاسبه کرد:
توجه داشته باشید که در رابطه فوق s برابر با نصف محیط مثلث (نصف مجموع طول سه ضلع) است.
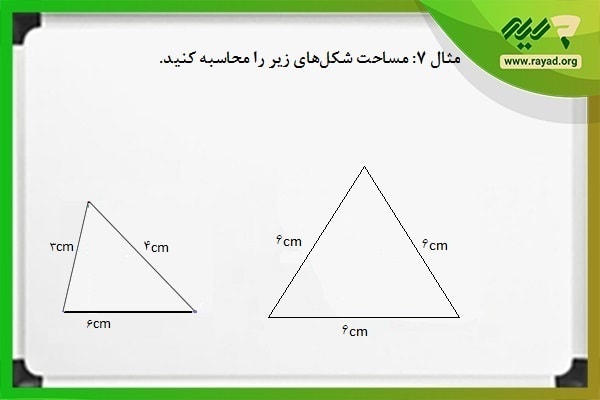
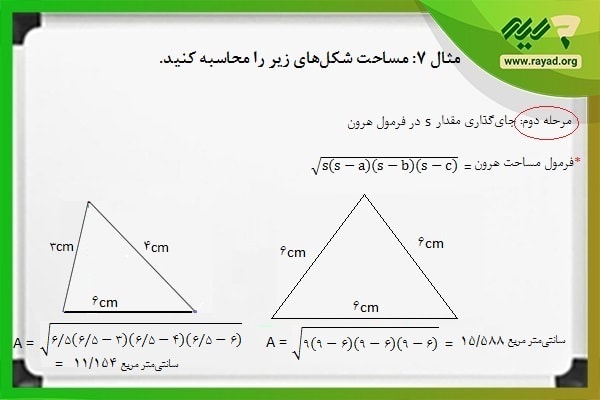
مثال ۷: مساحت شکلهای زیر را محاسبه کنید.
همانطور که گفتیم، برای محاسبه اندازه سطح مثلث بدون قاعده و ارتفاع و تنها از روی اندازه اضلاع آن از فرمول هرون استفاده میکنیم. به این ترتیب، ابتدا باید محیط مثلث را به دست آورده، آن را بر عدد ۲ تقسیم کرده و در نهایت در فرمول هرون جایگذاری کنیم. بر همین اساس، خواهیم داشت:
در نهایت، مقدار s را در فرمول هرون به صورت زیر جایگذاری میکنیم:
کلام آخر
در این مقاله ی آموزشی شما با محیط و مساحت مثلث آشنا شدید و به عبارتی متوجه شدید که محیط و مساحت مثلث چیست.
نظرات خودتان را با ما در رابطه با این بلاگ آموزشی در میان بگذارید.









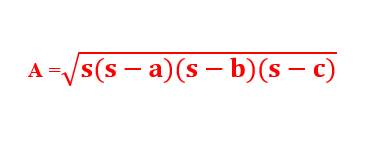

سلام و عرض ادب
من امروز یک روش دیگه برای محاسبه مساحت یاد گرفتم، خدا خیرتان بده، فقط فکر میکنم یک روش دیگه برای محاسبه مساحت باشه که بهش اشاره نکردید! محاسبه مساحت مثلث با داشتن دو ضلع و زاویه بین! که مساوی هست با دو ضلع ضربدر هم و ضربدر سینوس زاویه بین، تقسیم بر دو! اگر این درست هست، لطفا اطلاع بدید
با تشکر
فاطمی مرام
سلام دوست عزیز
ممنون از پیشنهاد و ارائه روش
محاسبه ی یکی از مثلثها اشتباهه
اونی که ۶/۵ را ضرب کردین
ممنونم که مطالب خوب رو ، رایگان در دسترس قرار میدید. خسته نباشید
سلام بیتا عزیز
ممنون از توجه شما.
اگر مثلث های دیگر هم بود بهتر میشد
سلام دوست عزیز
برای مشاهده مساحت و محیط مثلث ها با مثال های بیشتر بر روی لینک های زیر کلیک کنید:
مساحت و محیط مثلث متساوی الساقین
مساحت و محیط مثلث قائم الزاویه
مساحت و محیط مثلث متوازی الاضلاع
سپاس از مطالب خوب و کاربردی شما
خیلی خیلی راضی هستم چون مطالب خیلی خوبی را بیان کرده بودید
دوست عزیز ممنون از توجه شما